
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Нормальный закон распределения. Ответ: Нормальный закон распределения(закон Гаусса)
Ответ: Нормальный закон распределения(закон Гаусса). Непрерывная случайная величина Х имеет нормальный закон распределения с параметрами  и
и 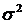 (обозначают
(обозначают 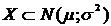 ), если ее плотность вероятности имеет вид:
), если ее плотность вероятности имеет вид:
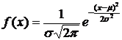 ,
где ,
где 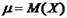 , ,  . .
| 
| 
|
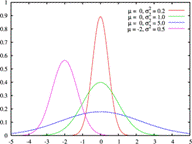
| Функция плотности вероятности f(x) | Функция распределения F(x) | |
| Рис.2. Нормальный закон распределения |
Математическое ожидание характеризует центр рассеивания значений случайной величины и при изменении  кривая будет смещаться вдоль оси абсцисс (см. рис. 2 при
кривая будет смещаться вдоль оси абсцисс (см. рис. 2 при  и при
и при  ). Если же при неизменном математическом ожидании у случайной величины изменяется дисперсия, то кривая будет изменять свою форму, сжимаясь или растягиваясь (см. рис. 2 при
). Если же при неизменном математическом ожидании у случайной величины изменяется дисперсия, то кривая будет изменять свою форму, сжимаясь или растягиваясь (см. рис. 2 при  :
:  ;
; 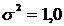 ;
; 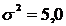 ). Таким образом, параметр
). Таким образом, параметр  характеризует положение, а параметр
характеризует положение, а параметр 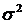 - форму кривой плотности вероятности. Нормальный закон распределения случайной величины Х с параметрами
- форму кривой плотности вероятности. Нормальный закон распределения случайной величины Х с параметрами  и
и  (обозначается N(0;1)) называется стандартным или нормированным, а соответствующая нормальная кривая – стандартной или нормированной. Согласно определению функция плотности вероятности и функция распределения связаны между собой:
(обозначается N(0;1)) называется стандартным или нормированным, а соответствующая нормальная кривая – стандартной или нормированной. Согласно определению функция плотности вероятности и функция распределения связаны между собой: 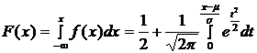 , где
, где  . Интеграл такого рода является "неберущимся", поэтому для его нахождения используют особую функцию, так называемый интеграл вероятностей или функцию Лапласа, для которой составлены таблицы (см. Приложение 1).
. Интеграл такого рода является "неберущимся", поэтому для его нахождения используют особую функцию, так называемый интеграл вероятностей или функцию Лапласа, для которой составлены таблицы (см. Приложение 1).
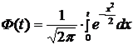 , ,
 - функция нечетная! - функция нечетная!
| 
|
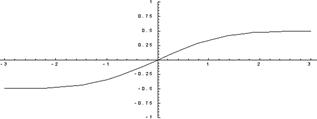
| Рис. 3. Функция Лапласа Ф(t) |
Используя функцию Лапласа можно выразить функцию распределения нормального закона по формуле:  , где
, где  . Для практических целей очень важны свойства случайной величины, имеющей нормальный закон распределения. 1)Если
. Для практических целей очень важны свойства случайной величины, имеющей нормальный закон распределения. 1)Если 
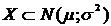 , то для нахождения вероятности попадания этой величины в заданный интервал (х1;х2) используется формула:
, то для нахождения вероятности попадания этой величины в заданный интервал (х1;х2) используется формула: 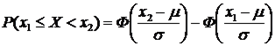 . 2)Вероятность того, что отклонение случайной величины
. 2)Вероятность того, что отклонение случайной величины  от ее математического ожидания
от ее математического ожидания  не превысит величину
не превысит величину  (по абсолютной величине), равна:
(по абсолютной величине), равна:  .
.
3)"Правило трех сигм". Если случайная величина 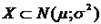 , то практически достоверно, что ее значения заключены в интервале (
, то практически достоверно, что ее значения заключены в интервале ( 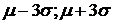 ). (Вероятность выхода за эти границы составляет 0,0027.) Правило позволяет, зная параметры (
). (Вероятность выхода за эти границы составляет 0,0027.) Правило позволяет, зная параметры (  и
и  ), ориентировочно определить интервал практических значений случайной величины. Пример 5. Случайная величина распределена нормально с параметрами
), ориентировочно определить интервал практических значений случайной величины. Пример 5. Случайная величина распределена нормально с параметрами  ,
,  . Найти вероятность того, что случайная величина в результате опыта примет значение, заключенное в интервале (12,5; 14).
. Найти вероятность того, что случайная величина в результате опыта примет значение, заключенное в интервале (12,5; 14).
 .
.
Пример 6. Случайная погрешность измерения подчинена нормальному закону распределения с параметрами  ,
,  . Проводятся три независимых измерения. Найти вероятность того, что погрешность хотя бы одного измерения не превосходит по абсолютной величине 3 мм. Вероятность того, что погрешность измерения в одном испытании не превышает 3 мм:
. Проводятся три независимых измерения. Найти вероятность того, что погрешность хотя бы одного измерения не превосходит по абсолютной величине 3 мм. Вероятность того, что погрешность измерения в одном испытании не превышает 3 мм:
 . Вероятность того, что эта погрешность измерения в одном испытании превышает 3 мм, равна:
. Вероятность того, что эта погрешность измерения в одном испытании превышает 3 мм, равна: 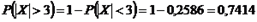 . Вероятность того, что во всех трех испытаниях погрешность измерения превышает 3 мм:
. Вероятность того, что во всех трех испытаниях погрешность измерения превышает 3 мм: 
 . Искомая вероятность:
. Искомая вероятность: 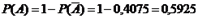 .
.
Дата добавления: 2015-01-19; просмотров: 221; Мы поможем в написании вашей работы!; Нарушение авторских прав |