Дисперсия и средне-квадратичное отклонение дискретной случайной величины.

Ответ: Во многих практически важных случаях существенным является вопрос о том, насколько велики отклонения случайной величины от ее математического ожидания.
Предварительно рассмотрим пример. Пусть две случайные величины и 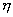заданы следующими рядами распределения:

Значения	-0,2	-0,1	0,1	0,2
	Вероятности p(x)	0,25	0,25	0,25	0,25

Значения	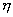-50	-40	40	50
Вероятности p(x)	0,25	0,25	0,25	0,25

Легко убедится в том, что математические ожидания этих величин одинаковы и равны нулю:

Однако разброс значений этих величин относительно их математического ожидания неодинаков. В первом случае значения, принимаемые случайной величиной , близки к ее математическому ожиданию, а во втором случае далеки от него. Для оценки разброса (рассеяния) значений случайной величины около ее математического ожидания вводится новая числовая характеристика - дисперсия.
Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математичекого ожидания *:

(43)

Пусть - дискретная случайная величина, принимающая значения x₁, x₂, ..., x_n соответственно с вероятностями p₁, p₂, ..., p_n. Очевидно, случайная величина принимает значения:

с теми же вероятностями p₁, p₂, ..., p_n. Следовательно, согласно определению математического ожидания дискретной случайной величины, имеем:

(44)

Если же - случайная величина с плотностью распределения , то по определению:

(45)

Принимая во внимание определение дисперсии и свойства математического ожидания, имеем:

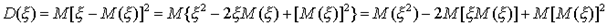
Так как и - постоянные, то используя свойства математического ожидания, получим: Следовательно, Откуда окончательно находим:

(46)

Рассмотрим теперь свойства дисперсии. 1°. Дисперсия постоянной равна нулю. (Доказательство)

2°. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:

(47)

(Доказательство)

3°. Если и 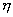- независимые случайные величины , то дисперсия суммы этих величин равна сумме их дисперсий:

(48)

(Доказательство)

Средним квадратическим отклонением случайной величины называется корень квадратный из ее дисперсии:

(49)

Среднее квадратическое отклонение имеет ту же размерность, что и случайная величина .