Типовые звенья САУ и их характеристики

К типовым звеньям относят звенья с наиболее простыми передаточными функциями (порядок числителя и знаменателя не превышает 2).

Типовые динамические звенья делятся на четыре группы по виду зависимости выходной величины x2 от входного воздействия x1 в установившихся режимах работы: 1) позиционные —выходная величина пропорциональна входному воздействию x2=Kx1; 2) интегрирующие — выходная величина пропорциональна интегралу от входного воздействия x2=K∫x1dt; 3)дифференцирующие — выходная величина пропорциональна первой производной по времени от входного воздействия x2=K dx1/dt; 4) запаздывающие — выходная величина равна входой величине, сдвинутой в текущем времени на время запаздывания τx2=x1(t –τ) [1, 2].

В переходных режимах работы динамические свойства звеньев и САУ определяются их временными и частотными характеристиками [1, 2]. Передаточные функции, переходные и весовые функции, амплитудно-фазовые характеристики (АФХ), амплитудные частотные характеристики (АЧХ), фазовые частотные характеристики (ФЧХ), логарифмические амплитудные (ЛАЧХ) и фазовые (ЛФЧХ) частотные характеристики типовых динамических звеньев приведены в таблице 1.2.1.

Тип звена и его передаточная функция	Временные характеристики позиционных звеньев
Переходная функция h(t)	Функция веса w(t)
1. Безынерционное W(p) = K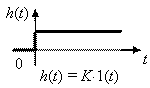
2. Апериодическое 1-го порядка W(p)=
3. Апериодическое 2-го порядка
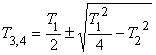
4. Колебательное q=1/T
Тип звена и его передаточная функция	Временные характеристики позиционных звеньев
Переходная функция h(t)	Функция веса w(t)
5. Идеальное W(p) = K/p, K = 1/T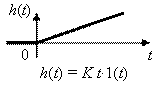
6. С замедлением
7. Изодромное
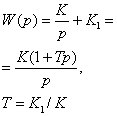
Временные характеристики дифференцирующих звеньев
8. Идеальное W(p) = K p
9. С замедлением
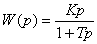
10. Форсирующее W(p) = K(1+Tp)
Временные характеристики звена запаздывания на постоянное время τ
11. Запаздывающее W(p) = e– τp
Частотные характеристики интегрирующих звеньев
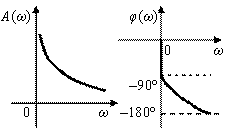
Амплитудно-фазовая	Амплитудная и фазовая	Логарифмические
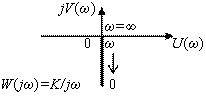
Частотные характеристики дифференцирующих звеньев
Частотные характеристики звена запаздывания на постоянное время τ

Дифференциальное уравнение процесса управления получается из (1.2.1) в виде:

(1.2.2)

где T — постоянная времени звена; K — коэффициент передачи звена.

Переходная функция звена h(t)=x2(t) получается в виде суммы общего и частного решений дифференциального уравнения (1.2.2) при нулевых начальных условиях и подаче на вход единичного ступенчатого воздействия x1(t)=1[t]

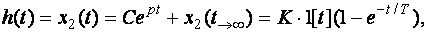(1.2.3)

где p=–1/T — корень характеристического уравнения Тр+1=0; С=–K