Перенос точки разветвления

x x₁ x₂ x x₁ x₂

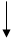
W₁(p) W₂(p) = W₁ (p) W₂(p)

® 1/W₂(p)

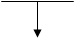x x₁ x₂ x x₁ x₂

W₁(p) W₂(p) = W₁ (p) W₂(p)

W₁(p)

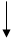
x₁

Рис. 5.7

Пример: систему, представленную на рис. 5.8, свести к одноконтурной и определить её передаточную функцию

W₃ W₅

y - Х_вых

Х_вх W₁ W₂

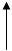W₄

Рис.5.8

Перенесём точку съёма сигнала y через звено W₁ против направления передачи сигнала (рис. 5.9). Очевидно, что звенья W₁ и W₄ включены пос-

W₃ W₅

y - Х_вых

Х_вх W₁ W₂

W₁ W₄

Рис.5.9

ледовательно, а W₁ и W₃ - параллельно. Поэтому W₆ = W₁ + W₃ ;

W₇ = W₁W₄ (рис.5.10).

W₅

y - Х_вых

Х_вх W₆ W₂

z

W₇

Рис. 5.10

Перенесём сигнал z через звено W₂ (рис. 5.11).

W₅

y - Х_вых

Х_вх W₆ W₂

W₇ 1 / W₂

Рис.5.11

Звенья W₇ и 1/W₂ включены последовательно, поэтому W₈ = W₇/ W₂ ,

по отношению к W₆ – параллельно: W₉ = W₆ + W₈ .

Звено W₂ охвачено отрицательной обратной связью, поэтому W₁₀ = W₂ / (1 + W₂W₅) . Эти два эквивалентных звена включены последовательно (рис. 5.12).

Х_вх Х_вых

W₉ W₁₀

Рис. 5.12

Аналогично можно преобразовывать и другие структурные схемы.

Таким образом, достаточно сложные системы можно свести к одноконтурной или к последовательному соединению звеньев, что существенно облегчает их анализ и построение характеристик.

ПРИМЕР: построить асимптотическую логарифмическую амплитудную частотную характеристику системы с передаточной функцией

100 (0,1p + 1)

W (p) = .

p (0,01p + 1) (0,001p + 1)

Предварительно проводим анализ системы.

Нетрудно убедиться, что данная система состоит из последовательного соединения интегрирующего, форсирующего идеального с постоянной времени t = 0,1 с и двух апериодических звеньев первого порядка с постоянными времени Т1 = 0,01 с и Т2 = 0,001 с. Передаточный коэффициент системы к = 100.

Следовательно, характеристика начинается в точке 20lg k = 20lg100 = 40. Наклон начального участка определяется астатизмом системы (есть или нет идеальные интегрирующие и дифференцирующие звенья). В нашем случае имеется интегрирующее звено, поэтому наклон начального участка –20дБ/дек. Первая частота сопряжения принадлежит звену с наибольшей посто-янной времени, в данном случае это постоянная идеального форсирующего звена t = 0, 1 с. Частота сопряжения w с1 = 1/t = 1/0,1 = 10 c^-1, наклон второй асимптоты + 20 дБ/дек, суммарный наклон –20 + 20 = 0 дБ/дек. Вторая частота сопряжения принадлежит апериодическому звену первого порядка с постоянной времени Т1 = 0, 01 и равна w с2 = 1/Т2 = 1/0, 01 = 100 с^-1, наклон третьего участка –20дБ/дек, суммарный наклон – 20дБ/дек. Третья частота сопряжения принадлежит апериодическому звену звену с постоянной времени Т2 = 0, 001 с, частота сопряжения w с3 = 1/Т2 = 1/0, 001 = 1000 с^-1, наклон четвёртого, последнего участка, уходящего в бесконечность, – 20дБ/дек, суммарный наклон – 40дБ/дек.

Асимптотическая логарифмическая амплитудно-частотная характеристика, построенная на основании этих расчётов, приведена на рис. 5.13

L(w)

40

-20

20

-20

10 100 1000

w

1 2 3 lgw

-40

Рис. 5.13

Наибольшая погрешность аппроксимации возникает на частотах сопряжения. Для оценки этой погрешности необходимо помнить, что:

1 дБ – это изменение А (ω ) на 12%

6 дБ ≈ в 2 раза

20 дБ ровно в 10 раз

В зарубежной литературе ЛАЧХ – это диаграмма Боде.

Сигнальные графы

Сигнальным графом называется множество узлов и множество направленных ветвей. Это графическое представление линейных алгебраических уравнений, показывающее взаимосвязь между переменными. Основным элементом сигнального графа является однонаправленный отрезок, называемый ветвью (рис. 5.14), который отражает зависимость между входной и выходной перемен-

W (p)

Х_ВХ (p) Х_ВЫХ (p)

Рис. 5.14

ной наподобие того, как это делает отдельный блок в структурной схеме. Каждый сигнал представлен узлом графа (точки входа и выхода), которые могут выполнять роль сумматора, а передаточная функция – ветвью со стрелкой. Сумма всех сигналов, входящих в узел, образует соответствующую этому узлу переменную. Сигнал, выходящий из ветви, равен передаточной функции этой ветви, умноженный на сигнал, входящий в ветвь.

Рассмотрим процедуру определения передаточной функции системы непосредственно по её графу, предварительно дав некоторые определения.

Узел – источник (исток) – это узел, из которого сигналы только вытекают, т.е. на всех ветвях, связанных с этим узлом, стрелки направлены от узла.

Узел – сток – это узел, в который сигналы только втекают.

Путь – это ветвь или непрерывная последовательность однонаправленных ветвей от одного узла к другому.

Прямой путь – это путь от истока к стоку, в котором ни один узел не встречается более одного раза.

Коэффициент передачи пути – произведение передаточных функций всех ветвей, образующих путь.

Контур – это замкнутый путь, который начинается и заканчивается в одном и том же узле, причём вдоль этого пути ни один другой узел не встречается дважды.

Некасающиеся контуры – это контуры, не имеющие общих узлов.

Коэффициент передачи контура – произведение передаточных функций всех ветвей, образующих контур.

Используя эти определения, можно привести формулу Мейсона , которая позволяет определить передаточную функцию только от истока к стоку и имеет вид

1 p

W (p) = ∑ P _k ∆ _k ,

∆ k =1

где ∆ - определитель графа;

∆ = 1 – (сумма коэффициентов передачи всех отдельных контуров) +

+ (сумма произведений коэффициентов передачи всех возможных

комбинаций некасающихся контуров, взятых по два) –

- (сумма произведений коэффициентов передачи всех возможных

комбинаций некасающихся контуров, взятых по три) + и т.д.;

Р_k – коэффициент передачи k прямого пути;

∆_k – определитель части графа;

∆_k = 1 – (сумма коэффициентов передачи всех отдельных контуров, не ка-

сающихся k пути) +

+ (сумма попарных произведений коэффициентов передачи всех

контуров, не касающихся друг друга и k пути) –

- (сумма тройных произведений коэффициентов передачи всех

контуров, не касающихся друг друга и k пути) + и т.д.

Рассмотрим в качестве примера систему с отрицательной обратной связью (рис. 5.15), передаточная функция которой равна

W_O (p)

W (p) = .

1 + W_OC (p) W_O(p)

X_ВХ(р) ∆Х Х_ВЫХ(р) Х_ВХ (р) 1 W_O(p) 1 Х_ВЫХ (р)

_ W_O(p)

- W_OC(p)

W_OC (p)

Рис.5.15

Сигнальный граф этой системы также представлен на рис5.15.

Нетрудно убедиться, что данный граф имеет один прямой путь с коэффициентом передачи

P₁ = W_O(p)

и один контур с коэффициентом передачи

L₁ = - W_OC (p) W_O (p).

Главный определитель графа

∆ = 1 - L₁ = 1 + W_OC (p) W_O (p),

а определитель части графа ∆₁ = 1. Следовательно,

P₁ ∆₁ W_O (p)

W (p) = = ,

∆ 1 + W_OC (p) W_O (p)

что совпадает с предыдущим результатом.

Несмотря на простоту данного примера, сигнальные графы следует применять осторожно, так как можно упустить из виду некоторые члены передаточных функций и к тому же не существует метода определения совершённых ошибок.

Очевидно также, что структурная схема и сигнальный граф несут одну и ту же информацию в графической форме.

Формулу Мейсона можно применять и непосредственно к структурной схеме. Надо всего лишь каждый термин, используемый при описании графа, перевести на язык описания структурных схем. При этом под сигналом следует понимать любой вход или любой выход блока или сумматора.