Устойчивость систем с запаздыванием

Отдельные звенья САР обладают “чистым” запаздыванием, которое сказывается в том, что система реагирует на входной сигнал не сразу, а по истечении некоторого постоянного времени t. Это обстоятельство учитывается введением звена чистого запаздывания с передаточной функцией

W(p) = exp (- t p),

а структурная схема системы показана на рис. 6.5.

х_вх W₀ (p) exp( - tp) х_вых

-

Рис. 6.5

Передаточная функция разомкнутой системы

W_р (p) = W₀ (p) exp (- tp).

Система без запаздывания (t = 0) называется предельной.

Частотные характеристики системы с запаздыванием и без него определяются, соответственно, выражениями

W_р (jw) = W₀ (jw) exp (- t jw);

W (jw) = W₀ (jw).

Отсюда видно, что для построения частотного годографа системы с запаздыванием следует построить годограф системы без запаздывания (предельной системы) и каждый вектор этого годографа повернуть по часовой стрелке на угол wt. Последний возрастает как при увеличении w, так и t.

Для некоторого значения t = t₀ и w = w_p годограф пройдёт через точку (-1, j0), и, следовательно, АСР будет находиться на границе устойчивости (рис. 6.6). Значения t₀ и w_p определяются из уравнения

W_p ( jw_p ) = W₀ ( jw_p ) exp ( -jw_p t₀) = -1.

Пространство параметров – плоскость Т₁ - к. Первая граница ( к = 0 ) лежит на оси Т₁. Вторая граница 1/Т₁ = к – 1/Т₂ имеет вид гиперболы с асимтотами Т₁ = 0 и к = 1/Т₁. Третья граница (Т₁ = 0) совпадает с осью к (рис. 6.9).

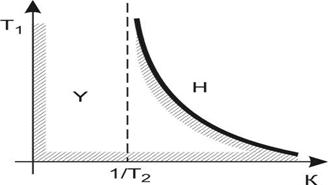
Рис. 6.9

Как видно из рисунка, при увеличении постоянных Т₁ и Т₂ область устойчивости сужается. Отрицательно влияет на устойчивость также и увеличение коэффициента усиления к. При любых заданных Т₁ и Т₂ существует своё к_кр.