Свойства монотонных последовательностей.

Ответ:

Определение. 1) Если x_n+1 > x_n для всех n, то последовательность возрастающая.

2) Если x_n+1 ³ x_n для всех n, то последовательность неубывающая.

3) Если x_n+1 < x_n для всех n, то последовательность убывающая.

4)Если x_n+1 £ x_n для всех n, то последовательность невозрастающая

Все эти последовательности называются монотонными. Возрастающие и убывающие последовательности называются строго монотонными.

Свойства монотонных последовательностей:

1. Пусть {a } – возрастающая (убывающая) последовательность, С – некоторое число. Тогда

а) {a +С} – возрастающая (убывающая) последовательность;

б) {Сa } – возрастающая (убывающая) последовательность при С>0;

в) {Сa } – убывающая (возрастающая) последовательность при С<0.

2. Если одна из последовательностей {a } и {b } возрастающая, а другая неубывающая, то{a +b } – возрастающая последовательность; если же одна из этих последовательностей убывающая, а другая невозрастающая, то {a +b } – убывающая последовательность.

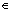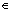3.а) Если одна из последовательностей {a } и {b } возрастающая, а другая неубывающая, то {a b } – возрастающая последовательность при a >0, b >0 для любых n N и {a b } – убывающая последовательность при a <0, b <0 для любых n N;

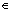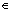б) если одна из последовательностей {a } и {b } убывающая, а другая невозрастающая, то {a b } – убывающая последовательность при a >0, b >0 для любых n N и {a b } – возрастающая последовательность при a <0, b <0 для любых n N.

4. Если {a } – возрастающая (убывающая) последовательность, то

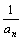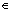а) { } – убывающая (возрастающая) последовательность при a >0 для любых n N;

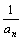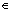б) { } – возрастающая (убывающая) последовательность при a <0 для любых n N.

5. Если все члены последовательности {a } принадлежат множеству M, которое содержится в области определения функции у=f(x), то

а) если {a } – возрастающая (убывающая) последовательность и функция у=f(x) возрастающая на множестве М, то {f(a )} – возрастающая (убывающая) последовательность;

б) если { 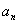} – возрастающая (убывающая) последовательность и функция у=f(x) убывающая на множестве М, то {f(a )} – убывающая (возрастающая) последовательность.

Например, из свойства 5 следует, что последовательности a = , b =lnn, с =n являются возрастающими, а последовательности a = , b =ln , с =( ) являются убывающими.