
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Бесконечно малые функции. Арифметические действия с бесконечно малыми (доказательство)
Ответ:
Пусть a(х), b(х) и g(х) – бесконечно малые функции при х ® а. Будем обозначать эти функции a, b и g соответственно. Эти бесконечно малые функции можно сравнивать по быстроте их убывания, т.е. по быстроте их стремления к нулю.
Например, функция f(x) = x10 стремится к нулю быстрее, чем функция f(x) = x.
Определение. Если  , то функция a называется бесконечно малой более высокого порядка, чем функция b.
, то функция a называется бесконечно малой более высокого порядка, чем функция b.
Определение. Если  , то a и b называются бесконечно малыми одного порядка.
, то a и b называются бесконечно малыми одного порядка.
Определение. Если 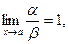 то функции a и b называются эквивалентными бесконечно малыми. Записывают a ~ b.
то функции a и b называются эквивалентными бесконечно малыми. Записывают a ~ b.
Пример. Сравним бесконечно малые при х®0 функции f(x) = x10 и f(x) = x.

т.е. функция f(x) = x10 – бесконечно малая более высокого порядка, чем f(x) = x.
Определение. Бесконечно малая функция a называется бесконечно малой порядка kотносительно бесконечно малой функции b, если предел 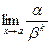 конечен и отличен от нуля.
конечен и отличен от нуля.
Однако следует отметить, что не все бесконечно малые функции можно сравнивать между собой. Например, если отношение 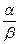 не имеет предела, то функции несравнимы.
не имеет предела, то функции несравнимы.
Пример. Если 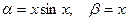 , то при х®0
, то при х®0  , т.е. функция a - бесконечно малая порядка 2 относительно функции b.
, т.е. функция a - бесконечно малая порядка 2 относительно функции b.
Пример. Если  , то при х®0
, то при х®0 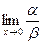 не существует, т.е. функция a и b несравнимы.
не существует, т.е. функция a и b несравнимы.
Свойства эквивалентных бесконечно малых.
1) a ~ a, 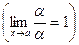
2) Если a ~ b и b ~ g, то a ~ g, 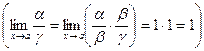
3) Если a ~ b, то b ~ a, 
4) Если a ~ a1 и b ~ b1 и  , то и
, то и 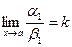 или
или 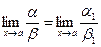 .
.
Следствие: а) если a ~ a1 и  , то и
, то и 
б) если b ~ b1 и  , то
, то 
Свойство 4 особенно важно на практике, т.к. оно фактически означает, что предел отношения бесконечно малых не меняется при замене их на эквивалентные бесконечно малые. Этот факт дает возможность при нахождении пределов заменять бесконечно малые на эквивалентные им функции, что может сильно упростить вычисление пределов.
Дата добавления: 2015-01-19; просмотров: 293; Мы поможем в написании вашей работы!; Нарушение авторских прав |