Переход к пределу в неравенствах для функций. Замена переменной при вычислении пределов.

Ответ:

Предельный переход в неравенстве.
Пусть в некоторой выколотой δ – окрестности точки х₀ функции f (x) и g (x) определены и выполнено неравенство f (x) < g (x). Пусть существуют пределы

и

тогда справедливо неравенство А ≤ B.
Доказательство. Пусть это не так,пусть А > B. Выберем как угодно малое положительное число ε таким, чтобы окрестности точек А и В не пересекались

(A – ε; A + ε ) ∩ (B – ε; B + ε ) ) = Ø

Кроме того по предположению

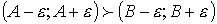
Знак между интервалами означает, что интервал (A - ε; A + ε) лежит правее интервала (B - ε; B + ε).
Из существования пределов функций f (x) и g (x) в точке х₀ следует

( ε > 0 ) ( δ₁ = δ₁ (ε) > 0, δ₁ < Δ) ( 0 < | x - x₀ | < δ₁ ) : | f (x) – A | < ε,

и

( ε > 0 ) ( δ₂ = δ₂ (ε) > 0, δ₂ < Δ) ( 0 < | x - x₀ | < δ₂ ) : | g (x) – B | < ε,

Если принять δ = min {δ₁,δ₂} < δ, то для 0 < | x - x₀| < δ следует неравенство f (x) > g(x). Но это противоречит условию теоремы, значит, наше предположение А > B неверное.

Часто при вычислении какого-либо предела естественно для упрощения выражения, от которого берётся предел, сделать некоторую замену переменного. Пусть, например, требуется вычислить

Тогда естественно с целью упрощения сделать замену 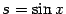: при этом функция, от которой берётся предел, упростится и будет иметь вид

.

Однако при этом нужно знать, как изменится база предела: что мы должны написать вместо

под знаком предела от функции ?

Рассмотрим общую ситуацию. Пусть (например, для упрощения выражения) предлагается сделать некоторую замену , при этом исходный предел вычислялся при базе , состоящей из некоторых окончаний . Тогда база множеств, которым принадлежит параметр 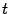, будет состоять из образов окончаний при отображении их функцией : надо посмотреть, куда перейдёт произвольное окончание старой базы при действии функции . 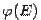Получится набор множеств , где множества состоят из всех таких точек 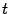, что при некотором .

Рис.2.12.Преобразование базы 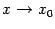под действием функции