Первый замечательный предел (доказательство)

Ответ:

Определение. Первым замечательным пределом называется предел Теорема. Первый замечательный предел равен

Доказательство . Рассмотрим два односторонних предела

и докажем, что каждый из них равен 1. Тогда по теореме 2.1 двусторонний предел также будет равняться 1. Итак, пусть (этот интервал -- одно из окончаний базы ). В тригонометрическом круге (радиуса ) с центром построим центральный угол, равный , и проведём вертикальную касательную в точке пересечения горизонтальной оси с окружностью ( 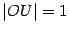). Обозначим точку пересечения луча с углом наклона с окружностью буквой , а с вертикальной касательной -- буквой ; через обозначим проекцию точки на горизонтальную ось.

Тригонометрический круг Пусть -- площадь треугольника , -- площадь кругового сектора , а -- площадь треугольника . Тогда очевидно следующее неравенство: 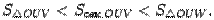Заметим, что горизонтальная координата точки равна , а вертикальная -- (это высота треугольника ), так что .

Площадь центрального сектора круга радиуса с центральным углом равна , так что . Из треугольника находим, что . Поэтому Неравенство, связывающее площади трёх фигур, можно теперь записать в виде Все три части этого неравенства положительны, поэтому его можно записать так: или (умножив на ) так: Предел постоянной 1 в правой части неравенства, очевидно, равен 1. Если мы покажем, что при предел в левой части неравенства тоже равен 1, то по теореме "о двух милиционерах" предел средней части также будет равен 1. Итак, осталось доказать, что . Сперва заметим, что , так как равняется длине дуги окружности , которая, очевидно, длиннее хорды . Применяя теорему "о двух милиционерах" к неравенству при , получаем, что Простая замена переменной показывает, что и . Теперь заметим, что . Применяя теоремы о линейности предела и о пределе произведения, получаем:

Тем самым показано, что Сделаем теперь замену ; при этом база перейдёт в базу (что означает, что если , то ). Значит, но ( -- нечётная функция), и поэтому Мы показали, что левосторонний предел также равен 1, что и завершает доказательство теоремы. Доказанная теорема означает, что график функции выглядит так: