
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основные теоремы о пределах функций. (доказательство)
Ответ:
Рассмотрим теоремы о правилах предельного перехода.
Т.1: Предел постоянной равен самой постоянной Доказательство следует из определения предела функции, так как  если с = const.
если с = const.
Т.2: (о связи функции с ее пределом). Для того чтобы 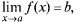 необходимо и достаточно выполнение равенства
необходимо и достаточно выполнение равенства  где
где 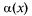 — б.м. при х
— б.м. при х  а
а 


Запишем цепочку равносильных утверждений, следующих из определения предела функции и определения б.м.:

Т.3: Предел суммы конечного числа функций, имеющих пределы при х  а, равен сумме их пределов
а, равен сумме их пределов
Пусть  тогда по теореме 2 име-
тогда по теореме 2 име-
ем  где
где  — б.м. при
— б.м. при
х 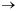 а, следовательно,
а, следовательно,  Используя лемму 1 о б.м., заключаем, что
Используя лемму 1 о б.м., заключаем, что  — б.м. при
— б.м. при
 и по теореме 2 получаем равенство
и по теореме 2 получаем равенство  b1 + b2
b1 + b2
Т.4: Предел произведения конечного числа функций, имеющих пределы при х 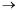 а, равен произведению пределов Методика доказательства аналогична доказательству Т.3. Следствие. Постоянный множитель можно выносить за знак предела.
а, равен произведению пределов Методика доказательства аналогична доказательству Т.3. Следствие. Постоянный множитель можно выносить за знак предела.
Т.5: Предел отношения двух функций, имеющих пределы при х 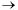 а, равен отношению их пределов (если предел знаменателя не нуль), т.е.
а, равен отношению их пределов (если предел знаменателя не нуль), т.е.

Пусть  тогда, используя Т.2, аналогично доказательству Т.3 запишем
тогда, используя Т.2, аналогично доказательству Т.3 запишем

где 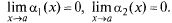 Числитель последней дроби по леммам о б.м. является б.м. Покажем, что
Числитель последней дроби по леммам о б.м. является б.м. Покажем, что  является функцией ограниченной, тогда дробь по лемме 2 о б.м. является б.м., и по Т.2:
является функцией ограниченной, тогда дробь по лемме 2 о б.м. является б.м., и по Т.2: 
Имеем в некоторой  окрестности т. а для любого
окрестности т. а для любого  > 0 вследствие справедливости
> 0 вследствие справедливости 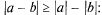

т.е. ограниченность  доказана
доказана
Дата добавления: 2015-01-19; просмотров: 420; Мы поможем в написании вашей работы!; Нарушение авторских прав |