
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Из шахты 3 $600, из шахты 4 $500.
Линейное программирование
Линейное программирование (ЛП) — это одна из математических задач оптимизации, которая широко применяется в инженерной деятельности.
Например, при выборе варианта технологического оборудования для изготовления тех или иных деталей желательно обеспечить их минимальную себестоимость [13]. Менеджеры предприятия, производящего несколько видов продукции, должны знать, сколько и какого вида продукции необходимо выпускать, чтобы доход был как можно больше или издержки как можно меньше [11]. С использованием ЛП решаются задачи перевозок, снабжения и многие другие.
2.6.1. Ограничения и целевая функция задач ЛП
Все модели ЛП имеют две основные составляющие части: целевую функцию и ограничения.
Целевая функция описывает некоторое количество, которое должно быть минимизировано или максимизировано. Например, целевая функция может иметь смысл цены продажи или затрат выпускаемой продукции какого-то предприятия. Возникает естественный вопрос: сколько и какого вида продукции необходимо изготовить предприятию, чтобы получить максимальную прибыль, или снизитьсебестоимость, время изготовления и т. д. При составлении задачи учитываются также ограничения на функционирование исследуемого объекта.
Пример.
Качество железной руды, добываемой на четырех шахтах, зависит от количества трех основных компонент, которые мы условно обозначим через А, В, С. В частности, каждая тонна руды должна содержать по крайней мере 5 кг элемента А, 100 кг элемента В и 30 кг элемента С. Содержание элементов в руде, добываемой в каждой из шахт, показано в таблице
Пример задачи ЛП Таблица 4.1
| № шахты | ||||
| компоненты руды | ||||
| содержание компонентов в 1 тонне руды в кг. | ||||
| А -(5) | ||||
| В-(100) | ||||
| С -(30) | ||||
| Цена руды $ |
Анализ приведенных данных показывает, что, например, руда из первой шахты удовлетворяет требованиям по содержанию элементов А и С, но не удовлетворяет требованиям по содержанию элемента В. Соответствующие выводы мы легко можем сделать и по остальным шахтам.
Очевидно, что для того, чтобы иметь руду, содержащую достаточное количество элементов А, В и С, необходимо смешивать руды из различных шахт. Это можно сделать разными способами.
Однако, руда из каждой шахты имеет свою цену, а именно:
одна тонна из шахты 1 стоит $800, из шахты 2 $400,
из шахты 3 $600, из шахты 4 $500.
Чем должен руководствоваться менеджер предприятия, покупающего руду? Естественно тем, чтобы цена была как можно меньшей и при этом, чтобы руда была необходимого качества. Данную реальную проблему можно сформулировать как математическую задачу.
Обозначим черезХ1количество руды, которое должно содержаться в одной тонне смеси, добываемой из шахты 1. Аналогично: Х2, — количество руды из шахты 2, Х3— количество руды из шахты 3, Х4 — количество руды из шахты 4.
Цена одной тонны смеси будет выражаться функцией:
 . (2.26)
. (2.26)
Выражение  будет определять содержание элемента А в одной тонне смеси. Так как это количество по условию должно быть не менее 5, то получаем:
будет определять содержание элемента А в одной тонне смеси. Так как это количество по условию должно быть не менее 5, то получаем:
 (2.27)
(2.27)
Точно также получим:
 (2.28)
(2.28)
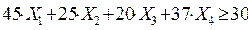 (2.29)
(2.29)
Необходимо учесть, что мы определяем смесь массой 1 тонна, т. е.
 (2.30)
(2.30)
Все величины Х1 , Х2 , Х3 , Х4должны быть неотрицательны.
 (2.31)
(2.31)
Итак, необходимо найти такие неотрицательные значения Х1, Х2, Х3, Х4, которые бы минимизировали функцию (2.26) и удовлетворяли бы ограничениям (2.28-.2.31).
Из выше изложенного следует, что задачи линейного программирования — это такие задачи, в которых целевая функция есть линейная функция, а ограничения — линейные равенства или неравенства.
2.6.2. Общая постановка задач ЛП
Как правило, большинство реальных проблем, которые можно сформулировать как задачи ЛП, имеют дело с достаточно большим количеством факторов. Поэтому приведем формулировку задач ЛП в общем виде, т. е. когда число неизвестных равноn, а число ограничений равно m.
Найти такие значения неизвестных х1, х2, . . . , хn, которые бы максимизировали (или минимизировали) целевую функцию
 ( 2.32)
( 2.32)
удовлетворяли бы ограничениям
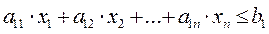 ,
,
…………………………………… (2.33)
 ,
,
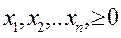 ( 2.34)
( 2.34)
Знак ≤ подразумевает, что ограничения могут иметь вид "=", "≥","≤".
Функция ( 2.32) есть целевая функция, (2.33) и (2.34) — ограничения задачи ЛП. Величины С1, С2, ..., Сп в выражении (2.32) называются коэффициентами целевой функции; aij (i=1, 2, . . . , m; j=l, 2, . . . , n) — коэффициенты условий (II. 2. 2); bi(i=1, 2, . . , т)— правые части ограничений
(2.33); условия (2.34) — условия неотрицательности.Из (2.33) и примеров, рассмотренных в предыдущем параграфе, следует, что ограничения могут быть неравенствами со знаками ≥ или ≤, а также иметь вид равенств. Соотношение между ти п, как правило, произвольно.
Все ограничения задачи образуют некоторую область в n-мерном пространстве, которую называют областью решенийили областью планов задачи ЛП.
Любая точка n-мерного пространства называется решениемили планом задачи ЛП, если ее координаты (х1, х2, . . . , хn) удовлетворяют всем ограничениям задачи ЛП.
План называется оптимальным, если его координаты обеспечивают минимум или максимум целевой функции.
Ограничения, имеющие первоначально вид неравенств, можно свести к равенствам. Для иллюстрации этой возможности вернемся к задаче, рассмотренной выше нами в предыдущем параграфе. В примере 1 ограничения имели вид

 ,
,
 , (2.35)
, (2.35)
 .
.
Правые части всех неравенства превосходят на какую-то неотрицательную величину левые части. Если мы к левым частям добавим новые неотрицательные переменные х3, х4 и х5 соответственно, то при определенных значениях этих неизвестных неравенства станут равенствами, т. е.

 ,
,


 , (2.36)
, (2.36)

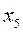

В примере 2 ограничения имели вид:
 ,
,
 , (2.37)
, (2.37)
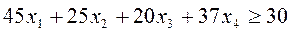 ,
,

Здесь уже левые части первых трех неравенств превосходят на какую-то неотрицательную величину правые части. Необходимо от левых частей отнять некоторые неотрицательные переменные х5, х6, х7 такие, что неравенства превратятся в равенства, т. е.
 ,
,
 , (2.38)
, (2.38)
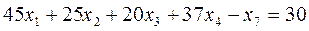 .
.
Понятно, что с последним ограничением примера никаких операций проделывать не надо. Переменные, которые надо прибавить к левым частям неравенств вида < или отнять от левых частей неравенств вида >, чтобы неравенства превратились в равенства, называются вспомогательными или дополнительными переменными.
Ясно, что значения дополнительных переменных не известны заранее. Введя дополнительные переменные, мы изменили задачу ЛП, т. к. у нас увеличилось число неизвестных. Мы должны эти новые неизвестные ввести в целевую функцию. Дополнительные переменные имеют конкретную интерпретацию.
Методы решения задач ЛП удобно применять в случае, когда ограничения были бы в форме равенств (речь не идет, конечно, об условиях неотрицательности). Если ограничения задачи ЛП записаны в виде неравенств, то говорят, что данная задача записана в стандартном виде. Если все ограничения имеют вид равенств,то говорят, что данная задача ЛП представлена в каноническом виде.
Можно использовать векторы и матрицы для записи задачи ЛП. Действительно, из коэффициентов ограничений aij без труда составляется матрица:
A = 
Запишем матрицы неизвестных, правых частей и целевой функции, соответственно
X =  , B =
, B =  ,
, 
. Тогда стандартную задачу ЛП можно записать так:
 , (П. 2. 4)
, (П. 2. 4)
 ,
,
 ,
,
или
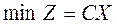 , (П. 2. 5)
, (П. 2. 5)
 ,
,
 ,
,
а если все ограничения в виде равенств (каноническая форма):
 ,(II. 2. 6)
,(II. 2. 6)
 ,
,
 .
.
Форма записи задачи ЛП в виде (П. 2. 1 - II. 2. 3) называется алгебраической формой задачи ЛП; форма записи в виде (II. 2. 4 — II. 2. 6) — матричной формой. Есть итретья форма записи — векторная.
Пусть С = (С1, С2, ... , Cn,), Х= (х1, х2,..., xn) соответственно вектор целевой функции и вектор неизвестных. Каждый столбец матрицы А и правые части обозначим через векторы:
A2 =  , A2 =
, A2 = 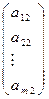 , ………. , An =
, ………. , An = 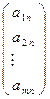 , B =
, B = 
Тогда задача ЛП будет иметь вид:
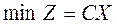
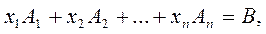
 .
.
Дата добавления: 2015-01-29; просмотров: 331; Мы поможем в написании вашей работы!; Нарушение авторских прав |