
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Упражнения. 1. Фирма изготовляет два вида лыж — беговые и слаломные
1. Фирма изготовляет два вида лыж — беговые и слаломные. Цифровые данные о возможностях фирмы в день приведены в таблице. Сколько пар лыж каждого типа должна производить фирма в день, чтобы прибыль была максимальной?
Таблица 2.6.2
| Количество человеко-часов для изготовления одной пары | Максимально возможное количество чел.- часов | |||
| беговые | слаломные | |||
| Изготавливающий цех | ||||
| Отделочный цех | ||||
| Прибыль за одну пару |
2. Предприятие ИВЦ «Техномаш» выпускает два вида огнетушителей – порошковые и аэрозольные. Цифровые данные о месячной производительности приведены в таблице. Сколько огнетушителей каждого типа должно производить предприятие в месяц, чтобы прибыль была максимальной?
| Количество нормо-часов для изготовления одного изделия | Максимально возможное количество нормо- часов | |||
| порош- ковые | аэрозоль- ные | |||
| Механо-сварочный цех | ||||
| Сборочный цех | 4 (2) | |||
| Прибыль за одно изделие $ |
3. Придумайте самостоятельно проблему, которую можно представить как задачу ЛП.
2.6.3. Геометрическая интерпретация задач ЛП
Если задача ЛП является задачей с двумя неизвестными х1и х2, то можно применить для ее исследования так называемый графический способ, основанный на геометрической интерпретации задачи ЛП.
Ограничения задачи ЛП определяют некоторую область в первой четверти плоскости xl0x2. Чтобы построить эту область (область планов задачи ЛП) необходимо графически решить систему неравенств, представляющих собой ограничения. Изобразим область допустимых решений задач ЛП.
Вы знаете, что любое линейное неравенство с двумя переменными делит плоскость на две полуплоскости, точки одной из которых удовлетворяют данному неравенству, точки другой — не удовлетворяют. Границей этих полуплоскостей является прямая, в уравнении которой левые и правые части такие же как и в данном неравенстве. Например, изобразим графически неравенство 

Рис. 2.13 Графическое изображение неравенства.
Алгоритм построения
1. Построили прямую 
2. Определили, что все точки, лежащие выше прямой, удовлетворяют данному неравенству. Для этого достаточно взять какую-нибудь точку из любой полуплоскости и проверить, удовлетворяют или нет ее координаты данному неравенству. Самое простое — взять точку О (0, 0).
0х1, — 0х2,<6.
Следовательно, точка О (0, 0) принадлежит множеству точек, удовлетворяющих данному неравенству. Если неравенство нестрогое, то точки прямой также будут удовлетворять неравенству.
Теперь ясно, как изобразить графически систему неравенств. Необходимо графически изобразить каждое неравенство, пересечение (общая часть) решений всех неравенств и будет изображать искомую область. Например, изобразим графически систему неравенств:

 ,
,
 , (2.39)
, (2.39)
 ,
,


Рис. 2.14 План задачи ЛП
Необходимо рассматривать только первую четверть, т. к. х1и х2 неотрицательны.
Решением данной системы является многоугольник, вершины которого находятся в точках (0, 0), (0, 10), (5, 8), (9, 4), (11, 0). Вершины многоугольника, являющегося решением данной системы неравенств определяются попарным решением линейных уравнений системы (2.39). Если данные неравенства суть ограничения задачи ЛП, то любая точка из полученного многоугольника (включая его границы) будет являться планом задачи ЛП.
Рассмотрим еще один пример. Изобразим графически решение следующей системы неравенств:

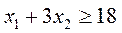 ,
,
 , (2.40)
, (2.40)
 ,
,

Дата добавления: 2015-01-29; просмотров: 282; Мы поможем в написании вашей работы!; Нарушение авторских прав |