Теорема III. 1.

Если план транспортной задачи является оптимальным, то ему соответствует система из т + п чисел

для (2.65)

для 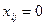(2.66)

(i = 1,2,..., т;j =1,2,..., п).

Строгое доказательство теоремы можно найти в большинстве учеб­ников по линейному программированию. Приведем лишь общие рас­суждения.

Числа и . называются потенциалами строк и столбцов соот­ветственно. Условия (2.65) есть не что иное, как система линейных уравнений для определения потенциалов, т. к. неравенства > 0 ха­рактерны только для занятых клеток. Условия (2.66) — условия оптимальности транспортной задачи. Согласно этим условиям вели­чины = 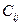— ( ) должны быть неотрицательными длянезанятых клеток в случае оптимального плана. Вспомним, как мы определяли величину, на которую изменится значение целевой функции при построении цепи. Например, для клетки 1С это значение будет равно:

(2.67)

Покажем, что Е_1С* = Е_1С Действительно,

В силу (III 3.1)

Подставим последние равенства в (III 3.3)

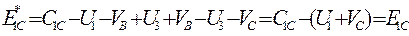
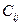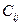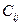Таким образом, если меньше алгебраической суммы потен­циалов своих строки и столбца, то перераспределение поставок по цепи к этой клетке уменьшает значение целевой функции. Наоборот, если больше то перераспределений к этой клетке увеличивает целевую функцию. Если = , то перераспределение к этой клетке не приведет к изменению целевой функции. Вам не напоми­нает это разности ?

Теперь становятся ясными этапы алгоритма получения опти­мального решения транспортной задачи.

1 этап. Находится первоначальный опорный план.

2 этап. Вычисляются потенциалы. Здесь надо иметь в виду, что

количество потенциалов т+п, а уравнений для их опре­деления п+т-1 (число занятых клеток). Поэтому од­ному из потенциалов (любому) придают какое-либо зна­чение, например, нулевое.

этап. Подсчитываются все для незанятых клеток. Если все , то найденный опорный план опти­мален, если есть , то строится цикл.

Пример решения транспортной задачи в Internet: Необходимо ежедневно с первого склада перевозить в два магазина 50 телевизоров , а со второго склада – 70. При этом первый магазин продает в день 40 телевизоров, а второй – 80 (50+70-40). В транспортной задаче неравенства в ограничениях заменены равенствами. Получается система линейных алгебраических уравнений с множеством решений, одно из которых оптимизирует целевую функцию. Известны затраты на перевозку одного телевизора со складов в магазины (четыре константы: 1200 у.е. при перевозке одного телевизора с первого склада в первый магазин, 1600 – с первого склада во второй магазин, 800 – со второго склада в первый магазин и 1000 – со второго склада во второй магазин).

Рис.2.24

Решите задачу о перевозке с 3 складов на 4 завода