Методы улучшения решения транспортной задачи. Критерий оптимальности

Мы научились строить первоначальный опорный план транспорт­ной задачи. Следующим этапом исследования будет рассмотрение воз­можностей улучшения первоначального решения. Естественно, что улучшить решение, т. е. уменьшить значение целевой функции, воз­можно только путем перераспределения груза из занятых клеток в какие-то незанятые. Возьмем первоначальное решение, полученное методом северо-западного угла.

Таблица 2.7.7

Рассмотрим первый ряд. Видно, что клетка с наименьшей стои­мостью в этом ряду 1С не занята. Естественно, возникает желание занять эту клетку. Поэтому мы:

1. Увеличим число единиц клетки 1С на 1. Пометим эту клетку значком "+", который поместим в нижний левый угол клетки.

2. Увеличение на 1 в клетке 1С необходимо компенсировать умень­шением в занятой клетке на 1 в первом ряду (или колонке С). Выберем клетку 1В. Пометим ее значком "—".

3. Нужно компенсировать уменьшение груза на 1 в клетке 1В. Это возможно сделать в клетках 2В или ЗВ. Предположим, выбира­ется клетка 2В. Но тогда в строке 2 станет больше количества груза, чем имеется в запасе в этой строке. Поэтому мы выбираем клетку ЗВ, т. е. в эту клетку добавляется единица груза и она помечается значком "+".

4. Чтобы не изменился баланс в третьем ряду (увеличили груз в клетке ЗВ), нужно уменьшить на 1 количество груза в остав­шихся занятых клетках этого ряда. Выберем клетку ЗС и пометим "—". Понятно, что выбрать таким образом клетку 3D мы не можем, т.к. при этом у нас нарушился бы баланс в столбце D, а компенсировать его нечем.

5. Уменьшение на 1 в клетке ЗС компенсируется увеличением на 1 в клетке 1С (шаг 1). Таким образом, баланс сохраняется везде.

Заметим, что клетки, помеченные знаком "+" и знаком "—", об­разуют замкнутую цепь. Это важный момент, который всегда нужно иметь в виду. В дальнейшем такую замкнутую цепь (или цикл) будем обозначать координатами помеченных клеток. В нашем случае — это 1С-1В + ЗВ-ЗС.

Чего же мы добились таким перераспределением? Давайте про­анализируем этапы нашей работы. Наглядно это можно представить в виде следующей схемы:

Действие Клетка Изменение целевой

функции

1. Увеличить на 1 1С +4

2. Уменьшить на 1 1В —13

3. Увеличить на 1 ЗВ +9

4. Уменьшить на 1 ЗС —12
Общее изменение —12

Вывод, к которому мы приходим: перераспределение на единицу груза, проведенное нами, приводит к уменьшению значения целевой функции на 12 единиц, т. е. улучшает ее значение. Становится ясным, что наше первоначальное решение не оптимально, раз оно может быть улучшено.

Вообще, цепи в транспортных задачах должны удовлетворять сле­дующим особенностям:

1. Цепь является замкнутым многоугольником. Если бы она была незамкнутой, то мы не могли бы перераспределить потоки груза с сохранением баланса по строкам или столбцам.

2. Все линии цепи — прямые, принадлежащие одной строке (или столбцу) матрицы транспортной задачи.

3. В цепи четное число вершин.

4. Для каждой начальной клетки цепи можно построить только одну цепь.

Мы начали перераспределение с клетки 1С. А если мы начнем с какой-либо другой клетки? Что будет при этом? Возьмем, например, цепь 1D —1В + ЗВ — 4D. Подсчитаем, какое изменение целевой функции произойдет:

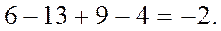
Значение уменьшится, но на меньшую величину, чем в первом случае.

Для примера еще рассмотрим какую-нибудь цепь: 2А — 2В + 1В — 1А.

В этом случае целевая функция изменится на:

т. е. увеличится. Аналогично можно сделать для любой незанятой клет­ки. Ясно, что перераспределения могут как увеличивать значение це­левой функции (что нам не надо), так и уменьшать (к чему нужно стремиться). Но неужели мы должны рассматривать все цепи? А как легче определить возможность улучшения найденного решения? Ины­ми словами, есть ли критерий оптимальности транспортной задачи? Ответ на этот вопрос дает следующая теорема: