Постановка транспортной задачи

Предположим, что некоторая компания имеет 4 завода, расположенных в разных пунктах (обозначим А, В, С, D). Необходимое сырье для выпуска продукции компания содержит на 3-х разных складах (обозначим 1, 2, 3). Известно, какое количество сырья требуется каждому заводу, например, в течение месяца. Заводу А необходимо 400т, В — 900т, С — 200т, D — 500т. Всего нужно 2000т. Также известно, что на первом складе находится 500т сырья, на втором — 700т, па третьем — 800т, т. е. общее количество — 2000т. И, наконец, существует информация о стоимости перевозки 1т сырья с любого склада на любой завод. Эти данные наглядно можно изобразить в виде матрицы

j A B C D

I

II

i III

Каждый элемент матрицы показывает стоимость перевозки одной тонны с соответствующего склада (строка матрицы) на конкретный завод (столбец матрицы). Так, например, число 10, стоящее во второй строке и в третьем столбце, показывает, что перевозка одной тонны со второго склада на завод С обойдется компании в $10. Так как запасов сырья столько же, сколько требуется заводам, то можно удовлетворить все потребности и, очевидно, существует много способов откуда, как и куда доставить это сырье.

Менеджер обязательно задастся целью: а как надо осуществить все перевозки, чтобы их общая стоимость была наименьшей? Он может потратить много времени, перебрав все возможные варианты, а может и использовать научный подход.

Давайте попробуем сформулировать данную проблему на языке математики. Рассматриваемая реальная ситуация очень напоминает нам конкретные ситуации, которые мы сводили к задачам ЛП.

Прежде всего нужно ввести переменные задачи. Обозначим через х_ij — количество сырья, которое перевозится из i — ого склада на j — ый завод. В нашем случае i = 1,2, 3; j = А, В, С, D. Так, например, x_2B — это количество тонн сырья, перевозимое со второго склада на завод В.

Подсчитаем стоимость перевозки всего сырья, например, с первого склада:

Аналогичным способом вычисляется стоимость перевозок и для других складов. Теперь ясно, как подсчитать стоимость всех перевозок, которую обозначим через Z

(2.48)

Функция Z есть не что иное, как целевая функция, которую нужно минимизировать и она линейная.

Перейдем к ограничениям. По условиям задачи известно, что с каждого склада должно быть вывезено все сырье. Это значит, что сумма всех х_ij (для каждой i — той строки) должна быть равной количеству сырья, находящемуся на i — ом складе, т.е.

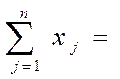
(2.49)

Кроме того, известно, что на каждый завод должно быть завезено определенное количество сырья, т.е.

(2.50)

Итак, мы имеем 3+4 = 7 ограничений и 3 • 4 = 12 переменных. Конечно, нужно учесть тот факт, что все х_ij не могут быть отрицательными. Таким образом, исходная проблема может быть сформулирована в форме задачи ЛП: