Построить самостоятельно

Чем отличаются решения систем неравенств (2.39) и (2.40)? В первом случае получаем многоугольник, т.е. ограниченное мно­жество; во втором область оказалась неограниченной. Итак, области планов задач ЛП могут быть как ограниченными, так и неограничен­ными.

Система неравенств в ограничени­ях задачи ЛП изображается, например, в виде двух областей?

Рис. 3.15 Неограниченная область планов задачи ЛП.

Этот случай соответствуеттому, что задача ЛП сформу­лирована неправильно, т. к. условия (I) и (III) (область (А)) противоре­чат условию (II) (область (Б)). Ясно, что здесь ни о каком решении речи быть не может. Этот случай называется несовместной задачей ЛП.

Передвигать параллельно эту прямую до тех пор, пока она не будет пересекать область допустимых планов задачи ЛП.

4) В случае задачи на максимум (минимум) эту прямую переме­щать в направлении вектора C (C₁,C₂) (противоположном), пока она не станет опорной. Любая точка опорной прямой и одновременно принадлежащая области допустимых планов и будет оптимальным решением.

Замечание.Этапы 2 и 3 можно объединить, т.е. сразу строить такую прямую, соответствующую какому-то зна­чению целевой функции, которая бы имела об­щие точки с областью допустимых планов.

Проиллюстрируем это на примерах. Рассмотрим следующую зада­чу ЛП:

,

,

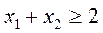, (2.41)

,

1) Строим область планов задачи:

Рис.2.17

2) Строим прямую

Рис.2.18

3) Передвигаем параллельно прямую по направле­нию вектора С (2,5). В точке В (пересечение третьей и вто­рой прямых) прямая А становится опорной.

Рис.2.19

Если бы мы двигали прямую (А) дальше, то значение целевой функции возрастало бы. Точка В является оптимальным планом дан­ной задачи и именно в ней целевая функция принимает наименьшее значение.

Отметим один факт. Если бы мы при данных ограничениях искали максимум функции Z, то найти его оказалось бы невозможным, т. к. область планов является неограниченной и целевая функция при дви­жении прямой Апо направлению вектора С неограниченно бы воз­растала.

Рассмотрим случай задачи на максимум:

Z=-6

,

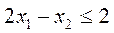, (2.42)

,

Изобразим область допустимых решений (треугольник ABC) и прямую (D), соответствующую нулевому значению целевой функ­ции, т. е. (рис.2.21)

Задача строится самостоятельно

Определив графически точки, в которых целевая функция имеет минимум (или максимум), можно найти координаты этих точек. Для этого надо решить систему из двух уравнений с двумя неизвестными x₁, x₂. Эти уравнения определяются прямыми, на пересечении кото­рых находится точка, являющаяся оптимальным планом.

В частности, в задаче (2.41) координаты точки В (Рис.2.19)определяются из системы уравнений (2.43)

(2.43)

Решение имеет вид (2.44)

(2.44)

Тогда:

В задаче (2.42) координаты В определяются из системы

(2.45)

Ее решение (Рис.2.21)

(2.46)

Из приведенных примеров интуитивно можно сделать вывод, что оптимальный план любой задачи ЛП находится в точке, являю­щейся одной из вершин множества допустимых решений. Такие точ­ки называются угловыми точками. Это действительно так. Вопрос: а как быть в случае, когда прямая, изображающая целевую функцию, становится опорной более чем в одной точке? Этот случай возможен только тогда, когда прямая, изображающая целевую функцию, параллельна одной из сторон многоугольника ре­шений, например, как на рисунке 2. 22, приведенном ниже.

,

(2.47)

Здесь прямая D соответствует нулевому значению целевой функции

Рис.2.22

В этом случае максимум (почему максимум?) целевой функции определяется координатами любой точки отрезка АВ, в том числе и координатами угловых точек А и В. Очевидно, что здесь имеет место случай, когда задача ЛП имеет множество решений (не путайте, по­жалуйста, с оптимальным значением целевой функции).

Графический способ решения задач ЛII применяется лишь в слу­чае, когда число неизвестных равно двум. В принципе, графически можно найти решения и для случая п = 3, но при этом необходимо строить плоскости в системе трех координат, наглядно изображать объемные картины. Во всех остальных случаях графический способ не применим (за исключе­нием некоторых случаев, когда п— т = 2).