
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод Фогеля
Метод, предложенный американским ученым У. Фогелем, является более сложным, но, в то же время, первоначальный опорный план этого метода наиболее близок к оптимальному. Идея метода основана на так называемом понятии штрафных затрат. Давайте выясним, что это такое. Обратим опять свое внимание к задаче ( ) — ( ), которую представим в виде таблицы:
Таблица 2.7.3
| А | В | С | D | Запас | Штраф | |
| 2 = 6 – 4 | ||||||
| 2 = 6 – 4 | ||||||
| 5 = 9 – 4 | ||||||
| Спрос | ||||||
| Штраф | 4 = 10 – 6 | 5=9-4 | 6 = 10 – 4 | 2 = 6 – 4 |
Рассмотрим ряд 1. Наименьшая цена доставки со склада 1 — это до завода С, и цена равна 4. Следующая наименьшая цена — до завода D. Она равна 6. Поэтому, если мы не будем посылать со склада 1 товар заводу С, то мы дополнительно понесем издержки, которые будут никак не меньше, чем 6 — 4 = 2. Это и будут штрафные затраты, которые записываются в дополнительный столбец таблицы 2.7.3 Аналогично определяются величины штрафных затрат всех остальных рядов, а также для всех колонок. Как видно из таблицы 2.7.3 наибольшая величина штрафа соответствует колонке С. Уделим этой колонке больше внимания, т. к. именно в этом случае понесутся наибольшие потери, если не будет использоваться клетка с наименьшей стоимостью. В этой колонке выбирается клетка с наименьшей ценой — клетка 1С и заполняется максимально возможным грузом. Возможно поместить только 200 т груза, в результате потребности завода С будут удовлетворены, но на складе 1 останется 500 — 200 = 300 т груза. В дальнейшем колонка С не рассматривается. Построим следующую таблицу:
Таблица 2.7.4
| А | В | С | D | Запас | Штраф | |
| 500-200 =300 | ||||||
| Спрос | ||||||
| Штраф |
Опять ищется ряд или колонка (без С), где штраф наибольший. Это 1 ряд. В этом ряду находится клетка с наименьшей ценой — клетка 1D и заполняется максимально возможным количеством товара. Из таблицы ясно, что в клетку помещается 300 т, т. к. такое количество товара осталось на складе 1. В результате запас склада 1 будет исчерпан, но заводу D необходимо еще 500 — 300 = 200 т. На следующих этапах ряд 1 и колонка С уже не будут учитываться. Следующая таблица будет иметь вид:
Таблица 2.7.5
| А | В | С | D | Запас | Штраф | |
| Спрос | ||||||
| Штраф |
Вам уже ясно, что делать дальше? Да, мы опять находим наибольшее значение штрафа (колонка D); в клетку 3Dзаносим 200 (почему?) и в дальнейшем исключаем из рассмотрения колонку D, т. к. спрос завода D удовлетворен.
Продолжая этот процесс, окончательно получаем таблицу (проделайте самостоятельно):
Таблица 2.7.6
| А | В | С | D | Запас | |
| Спрос |
В результате получился первоначальный опорный план данной задачи:

 все oстальные
все oстальные
Подсчитаем суммарные затраты:
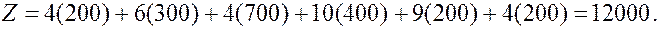
Опять же нет уверенности в том, что найденный план оптимален, хотя он, безусловно, лучше плана, полученного методом северо-западного угла.
Прежде чем мы перейдем к ответу на вопрос: а как определить, является ли данный опорный план оптимальным? — мы еще раз сформулируем основные этапы обоих алгоритмов.
Метод северо-западного угла:
1 Начинаем с клетки, находящейся в верхнем левом углу. Наполняем эту клетку максимально возможным грузом. Это количество определяется величинами спроса и запаса ряда 1 и первой колонки. Помещаемое количество груза равно меньшему значению спроса или запаса.
2 В зависимости от того, что использовано полностью (спрос или запас), переходим к соседней клетке. Это будет клетка, находящаяся в первом ряду и во втором столбце (если удовлетворен спрос), или клетка второго ряда и первого столбца (если использован запас).
3 Так же, как и в пункте 1 максимально заполняем следующую клетку.
4 Делаем аналогичные операции, как и в пунктах 2 и 3. Процесс продолжим до тех пор, пока все потребности полностью не удовлетворены и не исчерпаны все запасы.
Метод Фогеля:
1 Для каждого ряда и каждого столбца находим штрафные затраты путем вычитания наименьшей цены из следующей наименьшей цены.
2 Определяем ряд или столбец, где штрафные затраты наибольшие.
3 В выбранном в пункте 2 ряду или столбце заполняем максимально клетку с наименьшей стоимостью.
4 Возвращаемся к пункту 1, при этом ряд или столбец, выбранный в пункте 2, не учитывается.
5 Процесс повторяется до тех пор, пока все потребности не будут удовлетворены и все запасы не будут использованы.
Дата добавления: 2015-01-29; просмотров: 300; Мы поможем в написании вашей работы!; Нарушение авторских прав |