Формула наращения. В средне- и долгосрочных финансово-кредитных операциях, если проценты не выплачиваются сразу после их начисления

В средне- и долгосрочных финансово-кредитных операциях, если проценты не выплачиваются сразу после их начисления, а присоединяются к сумме долга, применяют сложные проценты. База для их начисления увеличивается с каждым шагом во времени. Процесс увеличения суммы долга происходит с ускорением. Наращение по сложным процентам можно представить как последовательные реинвестирования средств, вложенных под простые проценты на один период начисления. Присоединение начисленных процентов к сумме долга, которая послужила базой для их начисления, часто называют капитализацией процентов.

Если проценты начисляются и капитализируются один раз в году, то в конце первого года проценты составят Pi, а наращенная сумма – P + Pi = P (1 + i). К концу второго года наращенная сумма будет P (1 + i) + P (1 + i) i = P (1 + i)² и т. д. В конце n-го года

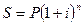, (3.1)

где n – число лет, i – процентная ставка.

Проценты за этот срок в целом таковы:

. (3.2)

Часть из них получена за счет начисления процентов на проценты. Она равна:

(3.3)

Рост по сложным процентам является процессом, соответствующим геометрической прогрессии с первым членом, равным P, и знаменателем (1 + i). Величину 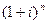называют множителем наращения по сложным процентам. Время при наращении по сложной ставке обычно измеряется как ACT/ACT.

Рис. 3.1

Пример3.1. Какой величины достигнет долг, равный 1 млн. руб., через 5 лет при росте по сложной ставке 15,5 % годовых?

По формуле (3.1) получим

руб.

Пример. Остров Манхэттен, на котором расположена центральная часть Нью-Йорка, был продан за 24 доллара. Стоимость земли этого острова через 350 лет оценивалась примерно в 40 миллиардов долларов, т. е. увеличилась в 1,667 ∙ 10⁹ раз. Такой рост достигается при сложной ставке всего 6,3 % годовых.

Формула 3.1 может применяться не только для годовой процентной ставки и срока, измеряемого в годах. Она используется и для периодов начисления, отличных от года. В этих случаях i означает ставку за один период начисления (месяц, квартал, полугодие), а n – число таких периодов [5, с. 43–45].

Если проценты на основной долг начисляются по ставке i, а проценты на проценты – по ставке r ≠ i, то

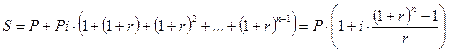. (3.4)