Принцип сжатых отображений. Решение нелинейных уравнений методом итераций. Оценка погрешности.

Если на множестве X задан оператор, то это записывается y=Ax, где А – символ оператора.

Если существует положительно число 0<α<1 , такое что для любых двух точек х и у пространства имеет место соотношение ρ(Ах,Ау)≤αρ(x,y), т.е. расстояние между образами≤расстоянию между прообразами, то оператор А называется оператором сжатия, а число α – коэффициентом сжатия.

Теорема о неподвижной точке – принцип сжатых отображений.

Если оператор сжатия А переводит точки n-мерного метрического пространства в точки того же пространства, то существует точка х* - неподвижная точка оператора, притом единственная. Итерационная последовательность, построенная для данного оператора с любым начальным приближением 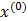, сходится к х*.

Путь требуется решить уравнение (1). Приведем уравнение (1) к виду (2), где - оператор, определенный на некотором замкнутом подмножестве E одномерного пространства действительных чисел. Если значение функции также принадлежит этому множеству, то можно строить итерационную последовательность с начальным приближением , т.е. ; ; … ; 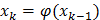. Если является оператором сжатия, то итерационная последовательность сходится и ее предел является корнем уравнения (2) и (1), причем согласно принципу сжатых отображений этот корень единичный.

Метод, основанный на рассмотрении и использовании итерационной последовательности называется методом итераций или методом последовательных приближений. . Поскольку в одномерном пространстве = , то формулы оценки погрешности k-го приближения:

или .

Если необходимо вычислить корень уравнения с точностью , то при построении итераций последовательности следует остановиться, если имеет место одно из неравенств: 1) ;

.

В этом случае за корень уравнения принимают k-е приближение.