Принцип сжатых отображений. Правило утроенного отрезка.

Если на множестве X задан оператор, то это записывается y=Ax, где А – символ оператора.

Если существует положительно число 0<α<1 , такое что для любых двух точек х и у пространства имеет место соотношение ρ(Ах,Ау)≤αρ(x,y), т.е. расстояние между образами≤расстоянию между прообразами, то оператор А называется оператором сжатия, а число α – коэффициентом сжатия.

Теорема о неподвижной точке – принцип сжатых отображений.

Если оператор сжатия А переводит точки n-мерного метрического пространства в точки того же пространства, то существует точка х* - неподвижная точка оператора, притом единственная. Итерационная последовательность, построенная для данного оператора с любым начальным приближением 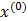, сходится к х*.

Теорема (2-е достаточное условие): Если

1) определена и дифференцируема на [a;b];

2) все ее значения также ;

3) существует такое, что ,

то итерационная последовательность этой функции с любым начальным приближением сходится и ее предел есть решение уравнения . Это уравнение на единственно.

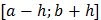Будем исследовать уравнение на промежутке , где h=|b-a| – длина промежутка.

Теорема (правило утроенного отрезка). Если

1) уравнение имеет единственный корень на промежутке длина ; 2) определена и дифференцируема на и все ее значения попадают на этот промежуток;

3) имеет место неравенство ;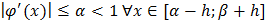

то итерационная последовательность с любым начальным приближением сходится, и ее предел является корнем . Корень на 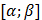единичный и для k-го члена итерационной последовательности применимы стандартные оценки погрешности.