
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Принцип сжатых отображений. Теоремы о достаточных условиях сходимости итерационной последовательности.
Если на множестве X задан оператор, то это записывается y=Ax, где А – символ оператора.
Если существует положительно число 0<α<1 , такое что для любых двух точек х и у пространства имеет место соотношение ρ(Ах,Ау)≤αρ(x,y), т.е. расстояние между образами≤расстоянию между прообразами, то оператор А называется оператором сжатия, а число α – коэффициентом сжатия.
Теорема о неподвижной точке – принцип сжатых отображений.
Если оператор сжатия А переводит точки n-мерного метрического пространства в точки того же пространства, то существует точка х* - неподвижная точка оператора, притом единственная. Итерационная последовательность, построенная для данного оператора с любым начальным приближением 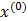 , сходится к х*.
, сходится к х*.
Теорема 1 (1-е достаточное условие): если функция  определена и дифференцируема на множестве
определена и дифференцируема на множестве  , причем существует
, причем существует  такое, что
такое, что  , то уравнение
, то уравнение  имеет решение, притом единственное. Это решение может быть получено методом последовательных приближений, причем за начальное приближение можно взять любое число
имеет решение, притом единственное. Это решение может быть получено методом последовательных приближений, причем за начальное приближение можно взять любое число  .
.
Доказательство: Функцию  можно рассмотреть, как оператор, определенный в пространстве
можно рассмотреть, как оператор, определенный в пространстве  с образом из того же пространства. Покажем, что
с образом из того же пространства. Покажем, что  является оператором сжатия. Возьмем 2 произвольные точки этого пространства и воспользуемся теоремой Лагранжа о конечных приращениях:
является оператором сжатия. Возьмем 2 произвольные точки этого пространства и воспользуемся теоремой Лагранжа о конечных приращениях:  Т.к.
Т.к. 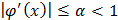 , то
, то  . Т.о.
. Т.о.  при условии
при условии  ,
,  является оператором сжатия. В силу теоремы о сжатых отображениях оператор
является оператором сжатия. В силу теоремы о сжатых отображениях оператор  имеет неподвижную точку
имеет неподвижную точку  , т.е.
, т.е.  . Эта точка единственна. Последнее равенство означает, что уравнение
. Эта точка единственна. Последнее равенство означает, что уравнение  имеет единственное решение, которое может быть получено, как предел итерационной последовательности.
имеет единственное решение, которое может быть получено, как предел итерационной последовательности.
Теорема 2 (2-е достаточное условие): Если  определена и дифференцируема на [a;b], все ее значения
определена и дифференцируема на [a;b], все ее значения  также
также  , существует
, существует  такое, что
такое, что  , то итерационная последовательность этой функции с любым начальным приближением
, то итерационная последовательность этой функции с любым начальным приближением  сходится и ее предел есть решение уравнения
сходится и ее предел есть решение уравнения  . Это уравнение на
. Это уравнение на  единственно.
единственно.
Доказательство: Отрезок 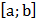 - замкнутое подмножество множества
- замкнутое подмножество множества  . (
. (  ,
,  ). Если в этом подмножестве ввести метрику так же, как и во множестве
). Если в этом подмножестве ввести метрику так же, как и во множестве  , то отрезок можно рассматривать, как метрическое пространство. Дальнейший ход рассуждений такой же, как и в теореме 1.
, то отрезок можно рассматривать, как метрическое пространство. Дальнейший ход рассуждений такой же, как и в теореме 1.
Дата добавления: 2015-01-29; просмотров: 329; Мы поможем в написании вашей работы!; Нарушение авторских прав |