Принцип сжатых отображений. Теорема о неподвижной точке.

Пусть даны два пространства Х и У и множество Е включающееся в Х. Если каждой точке х принадлежащей Е соответствует точка у принадлежащая У, то говорят, что на множестве Е определен оператор, при этом х – прообраз, а у – образ точки х.

у=Ах, где А-символ оператора.

Пусть дан оператор А, отображающий произвольную точку пространства Х в точку того же пространства. х=Ах – операторное уравнение. Решить такое уравнение - значит найти такое х*, точку n-мерного арифметического пространства, образ которой совпадает с этой точкой. Возьмем какую-либо точку 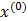из множества определения оператора А. Назовем ее начальным приближением. Найдем образ этой точки А и назовем первым приближением. Образ первого приближения обозначим , продолжая процесс, получаем последовательность точек 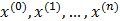,… n-мерного арифметического пространства, которая называется последовательностью приближений или итерационной последовательностью.

Если существует положительно число 0<α<1 , такое что для любых двух точек х и у пространства имеет место соотношение (Ах,Ау)≤α (x,y), т.е. расстояние между образами≤расстоянию между прообразами, то оператор А называется оператором сжатия, а число α – коэффициентом сжатия.

Теорема о неподвижной точке.

Если оператор сжатия А переводит точки n-мерного метрического пространства в точки того же пространства, то существует точка х* - неподвижная точка оператора, притом единственная. Итерационная последовательность, построенная для данного оператора с любым начальным приближением 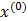, сходится к х*.

В качестве приближенного решения уравнения х=Ах можно выбрать k-ый член итерационной последовательности при этом будет использована следующие оценки погрешности:

( , ) =

( , ) = , где α-коэффициент сжатия.

Дата добавления: 2015-01-29; просмотров: 22; Нарушение авторских прав