N-мерное метрическое пространство, расстояние между точками.

Упорядоченную совокупность n действительных чисел называют точкой n-мерного пространства. Множество всех точек называют n-мерным арифметическим пространством.

Точку n-мерного арифметического пространства с фиксированными координатами будем обозначать

Пусть заданы две произвольные точки n-мерного арифметического пространства:

. Определим расстояние между этими точками. Способ введения расстояния между точками n-мерного арифметического пространства называется метрикой пространства.

Расстояние между двумя точками вводится чаще следующими тремя метриками:

(x,y)=max(|x₁-y₁|; |x₂-y₂|;…;|x_n-y_n|)

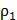(x,y)=|x₁-y₁|+|x₂-y₂|+…+|x_n-y_n|)

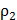(x,y)=

n-мерное арифметическое пространство с соответствующей метрикой обозначается , , . Очевидно, что расстояние между точками в различных метриках различны. Совпадают эти расстояния только при n=1.