Постановка задачи численного интегрирования. Формула Симпсона

При решении многих задач возникает необходимость вычисления определенных интегралов. Пусть требуется вычислить интеграл. Если для подынтегральной функции f(x) найдена первообразная F(x), то интеграл можно вычислить по формуле Ньютона-Лейбница: .

Однако, часто не бывает возможности использовать эту формулу, например, в следующих случаях:

1) Если первообразная функция F(x) не выражается в конечном виде через элементарные функции, так называемые не берущиеся интегралы:

2) Если первообразная функция F(x) имеет настолько сложную аналитическую запись, что ее использование не целесообразно.

3) Если подынтегральная функция f(x) задана графически или таблично.

Во всех этих случаях возникает необходимость разработки методов, позволяющих вычислять определенные интегралы приближенно. Эти формулы для вычисления приближенных интегралов называются квадратными.

Формула Симпсона или парабол.

Пусть требуется вычислить интеграл . Разобьем промежуток [a;b] на 2 равных отрезка, точками : ; .

Заменим подынтегральную функцию .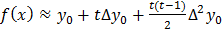

, тогда при 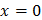, t=0; x= , t=2, тогда

Полученная формула называется формулой параболы или Симпсона.

Геометрический смысл формулы Симпсонасостоит в следующем: на промежутке [a;b] кривая y=f(x) заменяется параболой графиком интерполяционного многочлена.

Для получения более точного результата, необходимо промежуток [a;b] разбить на четное число равных частей, точками и применить к каждой паре смежных отрезков формулу парабол:

И применить к каждой паре смежных отрезков формулу Симпсона. Суммируя левые и правые части приближенных формул, получаем:

Абсолютная погрешность формулы Симпсона оценивается следующим образом: , где 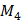– максимум модуля четвертой производной от подынтегральной функции на [a,b].

Очевидно, что оценка погрешностей квадратурных формул связана с нахождением производной и ее максимального значения на промежутке, и эта задача в вычислительной математике не всегда имеет адекватное решении. Поэтому погрешность квадратурных формул оценивается на практике с помощью двойного пересчета. Вычислим интеграл для n разбиений

И для 2n разбиений

Задача считается решенной, если