Геометрическая интерпретация сходимости итерационной последовательности.

Доказано, что достаточным условием сходимости итерационной последовательности к корню уравнения является выполнение следующего соотношения: . Рассмотрим 2 случая: 1) возрастает; 2) убывает.

1) Пусть .

На оси абсцисс произвольно выберем точку и проведем прямую, параллельно OY до пересечения с графиком . Через т. пересечения проведем прямую, параллельно оси OX до пересечения с 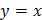. . Проведем через прямую, параллельно оси OY до пересечения с . Через точку пересечения параллельно оси OX – до пересечения с 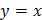. Проекция этой точку на ось OX есть ; ; . И т.д. Продолжая алгоритм, получим ломаную, звенья которой попеременно параллельны то оси OX, то OY. Если выбрано левее точки пересечения графиков, то приходится подниматься по «лестнице» вверх, в противном случае опускаться вниз.

2) Пусть .

Функция убывает, но не очень быстро, т.к. . Воспользуемся тем же алгоритмом, что и в п. 1. В случае отрицательной производной ломаная, построенная по алгоритму 1 представляет собой спираль, кот. Закручивается по мере приближения к т. пересечения графиков.

Оценка погрешности в случае убываний функции.

Рассматривая чертеж, убеждаемся, что в случае убываний функции корень уравнения всегда находится между 2-мя соседними приближениями. Теорема 4: если для ф-и выполнены условия по крайней мере одной из т-м 1, 2, 3, причем , то корень уравнения всегда заключен между любыми 2-мя сосед-ми членами итераций послед. Эта теорема дает простейшее правило оценки погрешности k-го приближения: . Если необходимо вычислить корень уравнения с точностью , то вычисление следует прекратить, как только 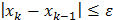. Тогда .