Обозначим

(13)

Теперь равенство (12) принимает вид:

(14)

т.е. задача свелась к отысканию приближающей функции в виде линейной. Практически для нахождения искомой приближающей функции в виде степенной (при сделанных выше предположениях) необходимо проделать следующее:

1. по данной таблице ( 1 ) составить новую таблицу, прологарифмировав значения x и y в исходной таблице;

2. по новой таблице найти параметры А и В приближающей функции вида (14);

3. использовав обозначения (13), найти значения параметров a и m и подставить их в выражение (11).

Необходимым условием для выбора степенной функции в качестве искомой эмпирической формулы является соотношение:

Показательная функция.Пусть исходная таблица (1) такова, что приближающую функцию целесообразно искать в виде показательной функции:

(15)

Прологарифмируем равенство (15):

(16)

Приняв обозначения (13), перепишем (16) в виде:

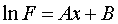(17)

Таким образом, для нахождения приближающей функции в виде (15) нужно прологарифмировать значения функции в исходной таблице (1) и, рассматривая их совместно с исходными значениями аргумента, построить для новой таблицы приближающую функцию вида ( 17). Вслед за этим в соответствии с обозначениями ( 13) остается получить значения искомых параметров a и b и подставить их в формулу (15).

Необходимым условием для выбора показательной функции в качестве искомой эмпирической формулы является соотношение:

.

Дробно-линейная функция. Будем искать приближающую функцию в виде:

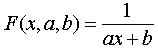(18)

Равенство (18) перепишем следующим образом:

Из последнего равенства следует, что для нахождения значений параметров a и b по заданной таблице (1) нужно составить новую таблицу, у которой значения аргумента оставить прежними, а значения функции заменить обратными числами, после чего для полученной таблицы найти приближающую функцию вида ax+b. Найденные значения параметров a и b подставить в формулу ( 18).

Необходимым условием для выбора дробно-линейной функции в качестве искомой эмпирической формулы является соотношение [38]:

.

Логарифмическая функция. Пусть приближающая функция имеет вид:

(19)

Легко видеть, что для перехода к линейной функции достаточно сделать подстановку lnx=u. Отсюда следует, что для нахождения значений a и b нужно прологарифмировать значения аргумента в исходной таблице ( 1 ) и, рассматривая полученные значения в совокупности с исходными значениями функции, найти для полученной таким образом новой таблицы приближающую функцию в виде линейной. Коэффициенты a и b найденной функции подставить в формулу (19).

Необходимым условием для выбора логарифмической функции в качестве искомой эмпирической формулы является соотношение:

.

Гипербола. Если точечный график, построенный по таблице (1), дает ветвь гиперболы, приближающую функцию можно искать в виде:

(20)

Для перехода к линейной функции сделаем подстановку .

(21)

Практически перед нахождением приближающей функции вида ( 20) значения аргумента в исходной таблице ( 1 ) следует заменить обратными числами и найти для новой таблицы приближающую функцию в виде линейной вида ( 21). Полученные значения параметров а и b подставить в формулу (20).

Необходимым условием для выбора уравнения гиперболы в качестве искомой эмпирической формулы является соотношение [38]:

.

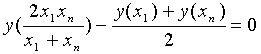Дробно-рациональная функция. Пусть приближающая функция находится в виде:

(22)

Очевидно, что

,

так что задача сводится к случаю, рассмотренному в предыдущем пункте. Действительно, если в исходной таблице заменить значения х и у их обратными величинами по формулам и и искать для новой таблицы приближающую функцию вида u=bz+a, то найденные значения а и b будут искомыми для формулы (22).

Необходимым условием для выбора дробно-рациональной функции в качестве искомой эмпирической формулы является соотношение [38]: