Состояние атома химическая связь

117. Некоторые проблемы периодической системы.

Тем не менее, в периодическом законе оставались некоторые проблемы. Предстояло определиться с местом в периодической таблице для двух групп элементов – инертных газов, имеющих нулевую валентность, и тринадцати редкоземельных элементов. Нельзя не упомянуть о том, что открытие большого числа элементов во второй половине XIX века было в значительной мере обусловлено появлением спектрального анализа, метода, который предложили в конце 1850-х годов немецкие учёные Густав Роберт Кирхгоф и Роберт Вильгельм Бунзен. В 1900-1902 гг. Д. И. Менделеев, Уильям Рамзай, первооткрыватель инертных газов, и Богуслав Браунер, известный своими работами по уточнению атомных масс химических элементов, произвели модернизацию периодической таблицы. Менделеев и Рамзай пришли к выводу о необходимости образования в таблице нулевой группы элементов, в которую вошли инертные газы. Нулевая группа прекрасно вписалась в периодическую таблицу; инертный газ явился элементом, переходным между галогенами и щелочными металлами. Браунер предложил решение проблемы размещения в таблице редкоземельных элементов. По его мнению, РЗЭ составляют особую группу периодической системы: "Подобно тому, как в Солнечной системе целая группа астероидов занимает полосу на месте пути, по которому должна бы двигаться одна планета, так точно целая группа элементов редких земель могла бы занять в системе одно место, на котором в другом случае стоит один элемент... Таким образом, все эти элементы, очень подобные один другому, стали бы на том месте в IV группе восьмого ряда, которое до сих пор занимал церий... Элементы редких земель создали бы особую интерпериодическую группу, аналогичную до некоторой степени восьмой группе, поместившись в середине остальных групп периодической системы..." Шестой период таблицы, таким образом, должен быть длиннее, чем четвёртый и пятый, которые в свою очередь длиннее, чем второй и третий периоды. В коротком варианте периодической таблицы Браунер предложил поместить все РЗЭ в одну клетку четвёртой группы.

118. Ковалентная связь, её особенности.

Ковалентная связь, атомная связь, гомеополярная связь (от лат. co — «совместно» и vales — «имеющий силу») — химическая связь, образованная перекрытием (обобществлением) пары валентных электронных облаков. Обеспечивающие связь электронные облака (электроны) называются общей электронной парой.

Особенность ковалентной связи состоит в том, что электронные пары, сформированные из неспаренных электронов свободных атомов, обобществляются атомными ядрами одинаковых или различных атомов. Ковалентная связь характерна для большинства химических соединений и прежде всего для многих простых веществ. Одной из простых молекул с ковалентной связью является молекула водорода. При образовании молекулы электроны, ранее принадлежавшие двум разным ядрам, обобществляются, образуя единое электронное облако. Каждой черточке соответствует электронная пара. Число электронных пар определяет валентность. [1]

Одной из особенностей ковалентной связи является ее поляризуемость. [2]Одной из особенностей ковалентной связи является возможность вращения соединенных ею атомов вокруг этой связиОдной из особенностей ковалентной связи является возможность вращения соединенных ею атомов вокруг этой связи.Одна из особенностей ковалентной связи заключается в том, что она обладает направленностью.

119. Квантовомеханическая модель (концепции), её варианты: методы валентных связей (ВС) и молекулярных орбиталей (МО).

В 1924 г. французский физик Луи де Бройль высказал идею о том, что материя обладает как волновыми, так и корпускулярными свойствами. Согласно уравнению де Бройля (одному из основных уравнений квантовой механики),

т. е. частице с массой движущейся со скоростью соответствует волна длиной X; — постоянная Планка.

Длину волны такой частицы называют длиной волны де Бройля. Для любой частицы с массой и известной скоростью длину волны де Бройля можно рассчитать. Идея де Бройля была экспериментально подтверждена в когда были обнаружены у электронов как волновые, так и корпускулярные свойства.

немецким ученым В. Гейзенбергом был предложен принцип неопределенности, согласно которому для микрочастиц невозможно одновременно точно определить и координату частицы X, и составляющую импульса вдоль оси х. Математически принцип неопределенности записывают следующими уравнениями:

Отсюда следует, что при точном определении координаты микрочастицы исчезает информация о ее импульсе так как при величина Если удастся снизить погрешность будет велика погрешность Источник этих погрешностей заключен не в приборах, а в самой природе вещей.

Поскольку постоянная Планка очень мала, то ограничения, накладываемые принципом неопределенности, существенны только в масштабах атомных размеров. Согласно принципу неопределенности, невозможно утверждать, что электрон, имеющий определенную скорость, находится в данной точке пространства, здесь можно использовать лишь вероятностное описание.

Для описания свойств электрона используют волновую функцию, которую обозначают буквой Квадрат ее модуля вычисленный для определенного момента времени и определенной точки пространства, пропорционален вероятности обнаружить частицу в этой точке в указанное время. Величину называют плотностью вероятности. Наглядное представление о распределении электронной плотности атома дает функция радиального распределения. Такая функция служит мерой вероятности нахождения электрона в сферическом слое между расстояниями от ядра. Объем, лежащий между двумя сферами, имеющими радиусы равен а вероятность нахождения электрона в этом элементарном объеме может быть представлена графически в виде зависимостей функции радиального распределения. На рис. 1.2 представлена функция вероятности для основного энергетического состояния электрона в атоме водорода. Плотность вероятности достигает максимального значения на некотором конечном расстоянии от ядра. При этом наиболее вероятное значение для электрона атома водорода равно радиусу орбиты соответствующей основному состоянию электрона в модели Бора. Различная плотность вероятности дает представление об электроне, как бы размазанном вокруг ядра в виде так называемого

Рис. 1.2. Радиальное распределение вероятности пребывания электрона для основного энергетического стояния атома водорода

Рис. 1.3. Электронное -облако

электронного облака (рис. 1.3). Чем больше величина , тем больше вероятность нахождения электрона в данной области атомного пространства.

В квантовой механике вместо термина «орбита» используют термин «орбиталь», которым называют волновую функцию электрона. Соответственно орбиталь характеризует и энергию и форму пространственного распределения электронного облака.

Расчеты в квантовой механике проводят с помощью предложенного в 1926 г. австрийским ученым Э. Шредингером уравнения, которое является математическим описанием электронного строения атома в трехмерном-пространстве.

В простейшем случае уравнение Шредингера может быть записано в виде

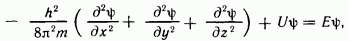
где — постоянная Планка; — масса частицы; — потенциальная энергия; Е — полная энергия; — координаты; — волновая функция.

Решая уравнение Шредингера, находят волновую функцию Решение уравнения Шредингера возможно лишь при определенных значениях полной энергии Е. Определив вероятностную функцию можно оценить величину — вероятность нахождения электрона в объеме пространства окружающего атомное ядро. Решение уравнения Шредингера представляет сложную математическую задачу.

Теория валентных связей (метод валентных связей, метод валентных схем, метод локализованных электронных пар) — приближённый квантовохимический расчётный метод, основанный на представлении о том, что каждая пара атомов в молекуле удерживается вместе при помощи одной или нескольких общих электронных пар.

Теория валентных связей заложена в 1927 году В.Гайтлером и Ф.Лондоном на примере квантовохимического расчёта молекулы водорода. В основе теории валентных связей лежит гипотеза о том, что при образовании молекулы из атомов, последние в значительной мере сохраняют свою электронную конфигурацию, а связывание атомов достигается в результате обмена электронов между ними и спаривания спинов двух электронов, находящихся на атомных орбиталях исходных атомов. Расчёт Гайтлера — Лондона оказался весьма значительным по своим результатам в развитии квантовой химии. В подтверждение электронной октетной теории (правило октета) Г.Льюиса было показано, что химическая связь в молекуле водорода действительно осуществляется парой электронов.

Метод молекулярных орбиталей исходит из того, что каждую молекулярную орбиталь представляют в виде алгебраической суммы (линейной комбинации) атомных орбиталей. Например, в молекуле водорода в образовании МО могут участвовать только 1s атомные орбитали двух атомов водорода, которые дают две МО, представляющие собой сумму и разность атомных орбиталей 1s1 и 1s2 – МО± = C11s1 ±C21s2.

Рисунок 3.6

Поскольку ядра во взаимодействующих атомах водорода одинаковы, то и вклад атомных орбиталей будет одинаковым, что обеспечивается равенством коэффициентов, с которыми s-орбитали участвуют в линейной комбинации (C1 = C2 = C). Поскольку должно выполняться требование, что сумма квадратов коэффициентов при АО равна 1, то имеем 2C2 = 1, откуда Опуская этот нормировочный множитель, запишем две молекулярные орбитали как сумму и разность АО атомов водорода:

Электронная плотность этих двух состояний пропорциональна |MO±|2. Поскольку в молекуле водорода взаимодействие возможно только по оси молекулы, то каждая из MO± может быть переобозначена как σсв = 1s1 + 1s2 и σ* = 1s1 – 1s2 и названа соответственно связывающей (σсв) и разрыхляющей (σ*) молекулярными орбиталями (рис. 3.7).

120. Двухатомные молекулы и ионы.

Двуха́томная моле́кула — молекула, составленная из двух атомов одного или разных элементов. Атомы связаны при помощи ковалентной связи.

Всего восемь элементов могут существовать в виде двухатомных молекул:

Водород H2

Азот N2

Кислород O2

Фтор F2

Хлор Cl2

Бром Br2

Иод I2

Астат At2

Двухатомные молекулы образуют только газообразные при обычных условиях элементы (за исключением инертных газов). То же относится и ко многим другим элементам в парах при достаточно высоких температурах.

Ио́н (др.-греч. ἰόν — идущее) — электрически заряженная частица (атом, молекула, свободный радикал), имеющая положительный или отрицательный заряд электричества, кратный заряду электрона. Положительно заряженный ион принято называть катионом, отрицательно заряженный ион - анионом.

121. Порядок (кратность) связи, её энергия и длина.

Характер распределения электронов по МО определяет порядок (кратность) связи, её энергию, межъядерные расстояния (длина связи), магнитные свойства молекул и др. Заполнение молекулярных орбиталей подчиняется тем же правилам, что и заполнение атомных: принципу энергетической выгодности,принципу Паули, правилу Хунда, принципу заполнения электронных структур Aufbau. В общепринятом приближении молекулярная орбиталь рассматривается как линейная комбинация атомных орбиталей (приближение МО ЛКАО).

Кратность связи в теории молекулярных орбиталей определяется выражением

где и — суммарные количества электронов на связывающих и разрыхляющих орбиталях соответственно.^[1]

122. Гетероядерные молекулы, полярность связи.

Гетероядерные молекулы можно изображать аналогично. Каждой паре электронов отвечает одна связывающая и одна разрыхляющая молекулярные орбитали; конкретный выбор атомных ор-биталей для образования молекулярных должен учитывать не только максимальное перекрывание и близость энергий атомных орбиталей, но и свойства их симметрии. Так, при образовании молекулы фтороводорода происходит перекрывание 1s - орбитали водорода и 2р - ор-битали фтора. [1]

Полярность химических связей — характеристика химической связи (как правило ковалентной), показывающая изменение распределения электронной плотности в пространстве вокруг ядер в сравнении с распределением электронной плотности в образующих данную связь нейтральных атомах.

Можно количественно оценить полярность связи в молекуле. Трудность точной количественной оценки состоит в том, что полярность связи зависит от нескольких факторов: от размеров атомов и ионов соединяющихся молекул; от числа и характера связи уже имевшихся у соединяющихся атомов до их данного взаимодействия; от типа структуры и даже особенностей дефектов их кристаллических решёток. Такого рода расчёты производятся различными методами, которые в общем-то дают примерно одинаковые результаты (величины). Например, для HCl установлено, что на каждом из атомов в этой молекуле имеется заряд, равный 0,17 заряда целого электрона. На водородном атоме +0,17, а на атоме хлора −0,17.

В качестве количественной меры полярности связи чаще всего используются так называемые эффективные заряды на атомах.

123. Многоатомные молекулы, их геометрическое строение.

Многоатомными считаются молекулы, образованные более чем двумя атомами. Начнем их рассмотрение с простой молекулы — молекулы СН₄.

В многоатомной молекуле можно указать центральный атом, с которого начинается построение энергетической диаграммы.

Для такого атома выделяется одна энергетическая ось. Энергетические диаграммы лигандов (лигандами называются атомы, ионы или молекулы, окружающие центральный атом (ион)) будем изображать все вместе на второй оси (рис. 15).

Рис. 15. Энергетическая диаграмма молекулы CH4

  Основные закономерности в геометрической конфигурации многоатомных молекул следуют из изложенных в разд. II понятий и постулатов классической теории. Они состоят в следующем. Фрагменты молекул, эквивалентные по их химическому строению, имеют приближенно одинаковую геометрическую конфигурацию независимо от молекулы, в которую они входят. Геометрическая конфигурация эквивалентных фрагментов в разных молекулах сохраняется в тем большей степени, чемдетальнее классификация фрагментов, согласно которой эти фрагменты приближенно эквивалентны. Таким образом, можно различать закономерности разных приближений, как это будет иллюстрировано ниже.[c.174]

124. Теории отталкивания валентных электронных пар (ОВЭП)

Теория отталкивания электронных пар валентных орбиталей (ОЭПВО) — один из подходов в химии, необходимый для объяснения и предсказания геометрии молекул. Согласно этой теории молекула всегда будет принимать форму, при которой отталкивание внешних электронных пар минимально (принцип минимума энергии).

Если бы природа сил взаимного отталкивания электронных пар имела чисто электростатический характер, эти силы определялись бы соотношением ( ), где 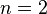. Однако кроме электростатического взаимодействия электронные пары на разных локализованных молекулярных орбиталях (ЛМО) испытывают отталкивание еще в силу действия принципа Паули, поэтому в выражении для сил , где — расстояние между «центрами тяжести» облаков электронных пар ЛМО, . Задача поиска расположения центров облаков электронных пар, расталкивающихся в соответствии с при равных для всех пар величинах , эквивалентна задаче размещения нескольких частиц на поверхности сферы при их максимальном удалении друг от друга. Эта задача решается строго для числа частиц от 2 до 12 и дает следующий результат:

Гибридизация орбиталей — гипотетический процесс смешения разных (s, p, d, f) орбиталей центрального атомамногоатомной молекулы с возникновением одинаковых орбиталей, эквивалентных по своим характеристикам.

sp-гибридизация[править | править вики-текст]

sp-гибридизация

Происходит при смешивании одной s- и одной p-орбиталей. Образуются две равноценные sp-атомные орбитали, расположенные линейно под углом 180 градусов и направленные в разные стороны от ядра центрального атома. Две оставшиеся негибридные p-орбитали располагаются во взаимно перпендикулярных плоскостях и участвуют в образовании π-связей, либо занимаются неподелёнными парами электронов.

sp²-гибридизация[править | править вики-текст]

sp²-гибридизация

Происходит при смешивании одной s- и двух p-орбиталей. Образуются три гибридные орбитали с осями, расположенными в одной плоскости и направленными к вершинам треугольника под углом 120 градусов. Негибридная p-атомная орбиталь перпендикулярна плоскости и, как правило, участвует в образовании π-связей

sp³-гибридизация[править | править вики-текст]

sp³-гибридизация

Происходит при смешивании одной s- и трех p-орбиталей, образуя четыре равноценные по форме и энергии sp³-гибридные орбитали. Могут образовывать четыре σ-связи с другими атомами или заполняться неподеленными парами электронов.

Оси sp³-гибридных орбиталей направлены к вершинам правильного тетраэдра, тогда как ядро центрального атома расположено в центре описанной сферы этого тетраэдра. Угол между любыми двумя осями приближённо равен 109°28'^[3], что соответствует наименьшей энергии отталкивания электронов. Также sp³-орбитали могут образовывать четыре σ-связи с другими атомами или заполняться неподеленными парами электронов.Такое состояние характерно для атомов углерода в насыщенных углеводородах и соответственно в алкильных радикалах и их производных.

125. Распределение электрического заряда в гетероядерных молекулах.

Гетероядерная двухатомная молекула, подобная НР, обладает    электрическим дипольным моментом, который обусловленпространственным разделением положительных и отрицательных зарядов. Если положительный и отрицательный заряды одинаковой абсолютной величины q находятся на расстоянии г друг от друга, это означает наличиедипольного момента ц (греческая буква  мю ), равного[c.536]

126. Электрический дипольный момент молекулы, влияние её геометрического строения, дипольных моментов связей и неподелённых электронных пар.

Электри́ческий ди́польный моме́нт — векторная физическая величина, характеризующая, наряду с суммарным зарядом (и реже используемыми высшими мультипольными моментами), электрические свойства системы заряженных частиц (распределениязарядов) в смысле создаваемого ею поля и действия на нее внешних полей. Главная после суммарного заряда и положения системы в целом (ее радиус-вектора) характеристика конфигурации зарядов системы при наблюдении ее издали.

Простейшая система зарядов, имеющая определенный (не зависящий от выбора начала координат) ненулевой дипольный момент — это диполь (две точечные частицы с одинаковыми по величине разноимёнными зарядами). Электрический дипольный момент такой системы по модулю равен произведению величины положительного заряда на расстояние между зарядами и направлен от отрицательного заряда к положительному, или:

где q — величина положительного заряда, — вектор с началом в отрицательном заряде и концом в положительном.

Для системы из N частиц электрический дипольный момент равен

где — заряд частицы с номером а — её радиус-вектор; или, если суммировать отдельно по положительным и отрицательным зарядам:

где — число положительно/отрицательно заряженных частиц, — их заряды; — суммарные заряды положительной и отрицательной подсистем и радиус-векторы их «центров тяжести»^{[прим 2]}.

Электрический дипольный момент нейтральной системы зарядов не зависит от выбора начала координат, а определяется относительным расположением (и величинами) зарядов в системе.

Из определения видно, что дипольный момент аддитивен (дипольный момент наложения нескольких систем зарядов равен просто векторной сумме их дипольных моментов), а в случае нейтральных систем это свойство приобретает еще более удобную форму в силу изложенного в абзаце выше.

127. Многоцентровые молекулярные орбитали.