
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
В. Обработка экспериментальных данных
По результатам замеров производится расчет требуемых величин по формулам.
1. Объем воды, вытекшей за время опыта, см3:
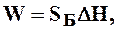
где 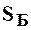 – площадь сечения мерного бака
– площадь сечения мерного бака 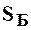 =5200см2;
=5200см2;
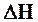 – приращение уровня воды в баке за время опыта, см.
– приращение уровня воды в баке за время опыта, см.
2. Расход воды, см3/с:
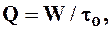
где 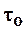 – время опыта.
– время опыта.
3. Средняя скорость движения воды, м/с:
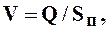
где 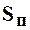 – площадь живого сечения потока воды, определяется как площадь поперечного сечения круглой трубы диаметром d = 5,7 см.
– площадь живого сечения потока воды, определяется как площадь поперечного сечения круглой трубы диаметром d = 5,7 см.
4. Кинематический коэффициент вязкости воды, Ст
(1 Стокс = 1 см2/с):
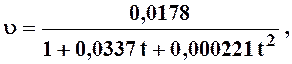
где t– температура воды в период опыта, °С.
5. Число Рейнольдса
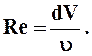
6. Максимальная скорость воды в трубопроводе (только для ламинарного режима), см/с:

где L – длина контрольного участка, см;
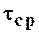 – среднее время прохождения частицами воды контрольного участка, с.
– среднее время прохождения частицами воды контрольного участка, с.
7. Коэффициент Кориолиса
.
Результаты расчетов вносятся в таблицу. По результатам расчетов в масштабе строится график зависимости Re = f (V) , на котором нужно показать зоны различных режимов движения и точки перехода от одного режима к другому.
Таблица 1.1
| Опыт | Режим течения воды | Приращение уровня в мерном баке | Время опыта | Объем вытекшей воды | Расход воды | Средняя скорость | Число Рейнольдса |
| DН, см | t, с | W, см3 | Q, см3/с | V, см/c | Re | ||
| Ламинарный | |||||||
| Начало переходного | |||||||
| Начало турбулентного | |||||||
| Турбулентный | |||||||
| Температура воды | t, °С | Максимальная скорость | Vmax, см/с | ||||
| Кинематический коэффициент вязкости | u, Ст | Коэффициент Кориолиса | a | ||||
| Время прохождения частицей струйки мерного участка | ti, c | tср, c |
Лабораторная работа № 2
Исследование уравнения Бернулли
Цель работы: знакомство с уравнением Бернулли, выяснение его геометрического и энергетического смысла и определение потерь напора в трубопроводе переменного сечения.
2.1. Теоретические положения
При установившемся течении жидкости на нее действуют силы тяжести, вязкости и давления. В 1738 году член Петербургской Академии наук Даниил Бернулли опубликовал капитальный труд по вопросам движения жидкости, положив начало гидродинамике. Уравнение Бернулли устанавливает зависимость между средней скоростью течения и силами, действующими в потоке жидкости. Для облегчения усвоения данного материала сначала рассмотрим случай течения элементарной струйки идеальной жидкости, а затем перейдем к потоку реальной жидкости.
А. Уравнение Бернулли для элементарной струйки
идеальной жидкости
Под идеальной жидкостью понимается такая воображаемая (условная) жидкость, которая совершенно лишена вязкости. В такой невязкой жидкости, так же как и в неподвижных реальных жидкостях, возможен лишь один вид напряжений – нормальные напряжения сжатия, т. е. гидромеханическое давление или просто давление.
Давление в движущейся идеальной жидкости обладает теми же свойствами, что и в неподвижной жидкости, т. е. на внешней поверхности жидкости оно направлено по внутренней нормали, а в любой точке внутри жидкости – по всем направлениям одинаково.
Возьмем одну из элементарных струек, составляющих поток, и выделим сечениями 1 и 2 участок этой струйки произвольной длины (рис. 2.1).
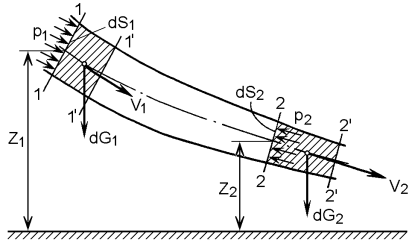
Рис. 2.1. Схема сил, действующих на элементарную струйку
идеальной жидкости
На струйку действуют силы давления p1S1 и p2S2 и силы тяжести G1 и G2.
Применив к массе жидкости в объеме рассматриваемого участка струйки теорему механики о том, что работа сил, приложенных к телу, равна приращению кинетической энергии этого тела, получим уравнение вида
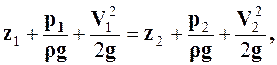 (2.1)
(2.1)
где z1 и z2 – высота расположения центров тяжести соответствующих сечений струйки от плоскости сравнения; V1, V2 – скорости струйки в соответствующих сечениях; r – плотность жидкости; g – ускорение свободного падения тела.
Полученное выражение и есть уравнение Бернулли для элементарной струйки идеальной жидкости.
Для выяснения геометрического смысла уравнения Бернулли рассмотрим размерности членов, составляющих его.
Гидростатический напор
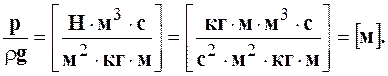
Гидростатический напор часто называют пьезометрическим вследствие того, что он может быть измерен при помощи пьезометрической трубки (пьезометра) (рис. 2.2, а).
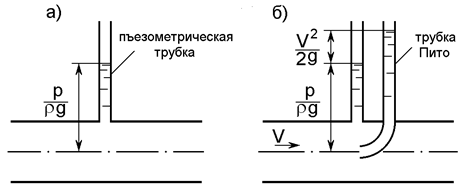
Рис. 2.2. Схемы измерения гидростатического и
скоростного напоров
Геометрический напор

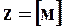 .
.
Скоростной напор
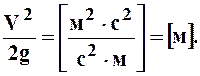
Скоростной напор можно измерить, добавив к пьезометрической трубке трубку Пито (рис. 2.2, б). Разность показаний этих двух трубок и даст значение скоростного напора.
Таким образом, мы имеем в каждом сечении струйки жидкости сумму трех напоров: гидростатического, геометрического и скоростного, т.е. полный напор, а уравнение Бернулли показывает, что полный напор в любом сечении элементарной струйки есть величина постоянная.
Энергетический смысл уравнения Бернулли можно установить, представив выражение (2.1) в другом виде, умножив все члены уравнения на g:
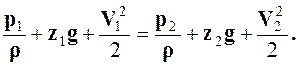
Рассмотрим размерность членов этого уравнения:
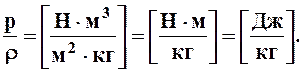
В числителе имеем размерность работы, а в знаменателе – массы. Таким образом, первый член уравнения Бернулли есть удельная (отнесенная к единице массы) энергия сил давления.
z g – представляет собой удельную энергию положения, так как частица массой m, находясь на высоте z , обладает энергией положения, равной:
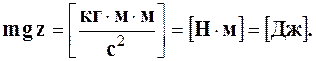
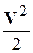 – удельная кинетическая энергия жидкости, так как для той же частицы массой m кинетическая энергия равна:
– удельная кинетическая энергия жидкости, так как для той же частицы массой m кинетическая энергия равна:
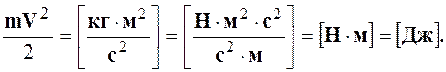
Таким образом, для элементарной струйки идеальной жидкости удельная энергия жидкости постоянная.
Графическая иллюстрация уравнения Бернулли для элементарной струйки идеальной жидкости представлена на рис. 2.3.
На рис. 2.3 необходимо обратить внимание на то, что линия полного напора располагается горизонтально, т. е. это постоянная величина.
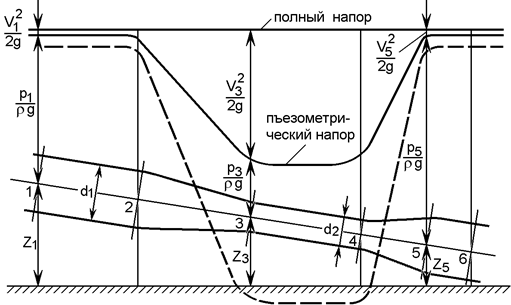
Рис. 2.3. Изменение пьезометрического и скоростного напоров
вдоль струйки идеальной жидкости
Б. Уравнение Бернулли для потока реальной жидкости
При переходе от элементарной струйки идеальной жидкости к потоку реальной (вязкой) жидкости, имеющему конечные размеры и ограниченному стенками, необходимо учесть неравномерность распределения скоростей по сечению потока, а также потери энергии (напора). То и другое являются следствием вязкости жидкости.
Неравномерность распределения скоростей по сечению потока учитывается коэффициентом Кориолиса:
a = 2 – для ламинарного режима течения жидкости;
a = 1,0…1,13 – для турбулентного режима течения жидкости.
Потери напора на участке между рассматриваемыми сечениями потока определяются в зависимости от характера сопротивлений на этом участке и подробнее будут рассмотрены в лабораторных работах № 3 и № 4.
Исходя из описанных условий, уравнение Бернулли для потока реальной жидкости имеет вид
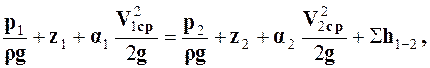 (2.2)
(2.2)
где a1 и a2 – коэффициенты Кориолиса для сечений 1 и 2;
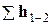 – суммарная потеря полного напора на участке между рассматриваемыми сечениями.
– суммарная потеря полного напора на участке между рассматриваемыми сечениями.
Графическая иллюстрация выражения (2.2) приведена на рис. 2.4.
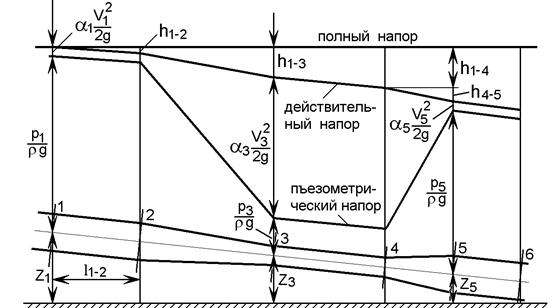
Рис. 2.4. Изменение пьезометрического и полного напоров
вдоль потока реальной жидкости
Из рисунка видно, что действительный напор в каждом последующем сечении уменьшается на величину потерь hi, затрачиваемых на трение жидкости.
2.2. Экспериментальная часть
А. Лабораторная установка
Лабораторная установка, позволяющая изучить изменение пьезометрического и скоростного напоров при течении воды по трубопроводу переменного сечения, состоит (рис. 2.5) из напорного бака 1 с пьезометром 3 и мерного бака 5, оснащенных измерительными устройствами, описанными в лабораторной работе № 1.
Регулирование расхода жидкости по трубопроводу 3 осуществляется вентилями 2 и 4. Трубопровод 3 установлен горизонтально и имеет три участка с различными внутренними диаметрами (d1, d2 и d3), соединенных плавными коническими переходами. На каждом участке установлены попарно пьезометрические трубки 6 и гидрометрические трубки Пито 7.
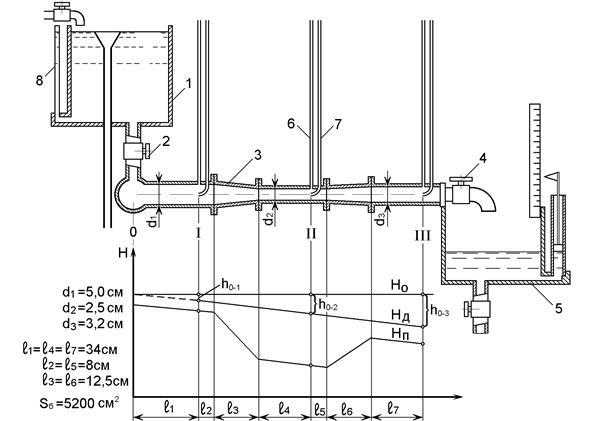
Рис. 2.5. Схема лабораторной установки
Б. Порядок проведения опытов
Для проведения опытов напорный бак заполняется водой, сливной вентиль мерного бака нужно закрыть. Эксперименты проводят при турбулентном режиме движения жидкости.
Вначале нужно полностью открыть вентиль 2 и, не открывая вентиль 4, снять показание измерительных трубок, соответствующее величине полного напора. Затем открыть вентиль 4 так, чтобы показания измерительных трубок находились примерно посередине или немного выше. По показаниям трубок убедиться, что наименьший пьезометрический напор (давление) и наибольший скоростной напор наблюдаются в участке трубопровода с меньшим сечением. Снять последовательно показания пьезометров и трубок Пито (с точностью до 0,5 сантиметра) на каждом участке. Одновременно при помощи секундомера определить время, за которое приращение уровня воды в мерном баке составит 3–5 см. Все результаты внести в таблицу (первый опыт). Для проведения следующего опыта нужно открыть вентиль 4 так, чтобы показания трубок уменьшились на 15–20 см. Последний опыт проводится при максимальном расходе, обеспечивающем показание пьезометров в пределах шкалы.
В. Обработка экспериментальных данных
1. Определить секундный расход воды
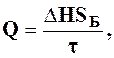
где SБ – площадь мерного бака (SБ = 5200 см2);
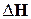 – приращение уровня в мерном баке, см;
– приращение уровня в мерном баке, см;
t – время опыта, с.
2. Определить среднюю скорость течения воды в каждом сечении трубопровода, см/с:
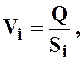
где 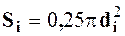 - площадь живого сечения трубопровода, см2.
- площадь живого сечения трубопровода, см2.
Здесь di – внутренний диаметр сечения трубы, см.
3. Определить скоростной напор в каждом сечении, см.
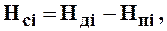
где 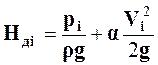 – показания трубки Пито в i-м сечении (действительный напор);
– показания трубки Пито в i-м сечении (действительный напор);
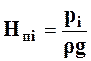 – показания пьезометрической трубки в i-м сечении (пьезометрический напор).
– показания пьезометрической трубки в i-м сечении (пьезометрический напор).
4. Определить среднюю скорость воды в сечениях по скоростному напору, см/с:
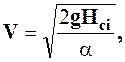
где a – коэффициент Кориолиса. Для турбулентного режима принять
a = 1,1.
5. Определить потери напора по участкам трубы, см:
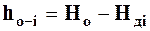 ,
,
где Ho – полный напор, см.
Результаты расчетов внести в таблицу 2.1.
По результатам замеров построить графики напоров для первого и последнего опытов, иллюстрирующие геометрический смысл уравнения Бернулли. Графики в отчете разместить после таблицы замеров на целой странице либо на миллиметровой бумаге, что предпочтительнее. Каждый график строится отдельно. Пример графика показан на рис. 2.5.
Таблица 2.1
| Опыт | Изменение уровня воды за опыт | Время опыта | Секундный расход воды | Полный напор | Сечения трубы | Скорость потока воды по расходу | Показания пьезометричес-кой трубки | Показания трубки Пито | Скоростной напор | Скорость потока воды по напору | Потери напора по сечениям трубы |
| № | 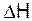 , см , см
| t, с | Q, см3/c | Ho, см | № | Vi, см/с | Нпi, см | Ндi, см | Нсi, см | Vi, см/с | h0-i, см |
Лабораторная работа № 3
Дата добавления: 2015-04-18; просмотров: 302; Мы поможем в написании вашей работы!; Нарушение авторских прав |