
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
В. Обработка экспериментальных данных. 1. Вычислить расход жидкости во всех опытах по формулам
1. Вычислить расход жидкости во всех опытах по формулам
 , см3/с (в табл. 4.1 и табл. 4. 3);
, см3/с (в табл. 4.1 и табл. 4. 3);
 , см3/с (в табл. 4.2);
, см3/с (в табл. 4.2);
где Sб – площадь мерного бака (Sб = 5200 см2).
2. Определить потери напора по формулам:
 см (в табл. 4.1);
см (в табл. 4.1);
 см (в табл. 4.2);
см (в табл. 4.2);
 см (в табл. 4.3).
см (в табл. 4.3).
3. Определить сопротивление трубопровода Аi по каждому опыту (табл. 4.1), с2/см5:
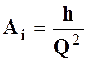
и среднее значение А для короткого (Ак) и длинного (Адл) трубопроводов.
4. Определить коэффициент Дарси l, исходя из того, что разность сопротивлений трубопроводов обусловлена их различной длиной, т. е.

Используя формулу (4.9), запишем

Отсюда


5. Пользуясь формулами (4.5) и (4.6), вычислить сумму коэффициентов местных сопротивлений длинного и короткого трубопроводов (xдл, xк).
6. Определить эквивалентную и расчетную длину (lэкв, L) трубопроводов по формулам (4.7) и (4.8).
7. Определить сопротивление полностью открытого вентиля (Ав) и его коэффициент сопротивления (xв), пользуясь формулами:


где dв– проходной диаметр вентиля, см.
8. Получить аналитическое выражение гидравлической характеристики системы, состоящей из параллельных трубопроводов и последовательно присоединенного вентиля, пользуясь формулами (4.6), (4.10) и (4.11).
Конечная формула имеет вид

а после подстановки численных значений Адл, Ак, Ав:

где Аp – полное сопротивление гидравлической сети.
При полученной формуле вычислить расчетные значения потерь напора ( hр ) при расходах, полученных в опытах, и результаты внести в табл. 4.3.
9. Построить совмещенные графики гидравлических характеристик короткого и длинного трубопроводов ( hк = AкQ2 и hдл = AдлQ2 ), характеристику вентиля ( hв =AвQ2 ), характеристики последовательного ( hпосл = AпослQ2 ) и параллельного ( hпар = AпарQ2 ) соединений исследованных трубопроводов и путем графического сложения характеристик hпар = AпарQ2 и hв =AвQ2 получить характеристику сети (hс = AсQ2). Построить характеристику сети по результатам расчетов (hр = AрQ2). Результаты можно считать удовлетворительными, если отклонение hс от hр не превышает 15%.
Таблица 4.1
| Опыт | Время опыта | Объем вытекшей воды | Расход жидкости | Показания пьезометра | Потеря напора | Сопротивление трубопровода | ||
| № | t, с | W, см3 | Q, см3/c | h1, см | h2, см | h, см | Ai | Aк; Aдл |
| Короткий трубопровод lк = , см; d = см | ||||||||
| Длинный трубопровод lдл = , см; d = см | ||||||||
Таблица 4.2
| Опыт | Время опыта | Приращение уровня в мерном баке | Расход воды | Показания пьезометра | Потеря напора на вентиле | Сопротивление вентиля |
| № | t, с | DH, см | Q, см3/c | h2, см | hв, см | Aвi |
| Среднее сопротивление вентиля | Aв | |||||
| Коэффициент сопротивления вентиля | xв |
Таблица 4.3
| Опыт | Время опыта | Объем вытекшей воды | Расход воды | Показания пьезометра | Потери напора в трубопроводе | Расчетное значение потерь напора |
| № | t, с | W, см3 | Q, см3/c | h1, см | h, см | hр, см |
| .... | ||||||
Лабораторная работа № 5
Истечение жидкости через отверстия и насадки
Цель работы: экспериментальное определение коэффициентов истечения воды через отверстия различной формы в тонкой стенке и через насадки; визуальное наблюдение эффекта Коанда и процесса инверсии струи из некруглых отверстий.
5.1. Теоретические положения
Истечение жидкости через малое незатопленное отверстие в тонкой стенке. Малым называется отверстие, вертикальный размер которого составляет не более 10 % глубины его погружения. В этом случае скорость входа частиц жидкости на верхней и нижней кромках можно считать одинаковой. При истечении жидкости в газовую среду, например в атмосферу, отверстие называют незатопленным. Тонкой считается стенка, если вытекающая жидкость касается лишь кромки отверстия, обращенной внутрь резервуара.
К основным рассчитываемым параметрам отверстий относят скорость истечения и расход жидкости. На их величину влияют действующий напор или эквивалентный ему перепад давления на отверстии, размеры и форма отверстия, его расположение относительно стенок, дна резервуара и свободной поверхности, свойства жидкости и режим ее истечения.
Рис. 5.1.Схема истечения жидкости через отверстие в тонкой стенке 
|
Истечение сопровождается эффектом сжатия струи, механизм которого поясняется рис. 5.1 на примере круглого отверстия в тонкой стенке.
Траектории частиц при приближении к отверстию искривляются. Возникающая при криволинейном движении частиц жидкости центробежная сила направлена внутрь формирующейся струи, вследствие чего уменьшается ее поперечный размер, т.е. происходит сжатие струи.
На входе в отверстие движение, установившееся при Н = const, неравномерное, а живое сечение существенно криволинейное и постепенно уменьшающееся по площади до наиболее сжатого сечения. По мере удаления от стенки кривизна линий тока уменьшается и на расстоянии » 0,5do от стенки линии тока практически параллельны. В силу малости отверстия местные скорости частиц можно считать одинаковыми, а коэффициент неравномерности скоростей (коэффициент Кориолиса) a®1.
Дальнейшее движение незатопленной струи является плавно изменяющимся под действием сил тяжести, инерции, поверхностного натяжения и трения. На значительном удалении от отверстия в связи с насыщением воздухом (аэрация) струя начинает дробиться и теряет компактность.
Различают полное и неполное, совершенное и несовершенное сжатие струи. Неполное сжатие наблюдается в тех случаях, когда струя подвергается сжатию не по всему периметру. Например, когда отверстие примыкает к дну (отсутствует сжатие с нижней стороны) или когда отверстие примыкает к дну и расположено у стенки резервуара (отсутствует сжатие с двух сторон).
Совершенным называется сжатие, когда отсутствует влияние свободной поверхности жидкости или твердых границ резервуара на поле скоростей частиц на входе в отверстие. Для выполнения этого условия расстояние от любой стенки (дна) резервуара или от свободной поверхности до ближайшей кромки отверстия должно быть не менее 3do.
Количественно эффект сжатия оценивается коэффициентом сжатия:
 , (5.1)
, (5.1)
где fc и fо – площади соответственно струи в сжатом сечении и отверстия. Для круглого отверстия  .
.
Расход жидкости через отверстие равен произведению скорости струи V на ее площадь:
 (5.2)
(5.2)
Теоретическая величина скорости струи определяется по формуле Торричелли, которая справедлива для идеальной жидкости:
 (5.3)
(5.3)
Фактическая величина скорости всегда меньше вследствие сопротивления отверстия (коэффициент сопротивления x ) и неравномерного распределения скоростей, оцениваемого коэффициентом Кориолиса a.
На основе уравнения Бернулли можно показать, что поправочный коэффициент на скорость истечения (коэффициент скорости) равен
 (5.4)
(5.4)
и тогда
 (5.5)
(5.5)
Произведение коэффициентов сжатия и скорости называют коэффициентом расхода:
 (5.6)
(5.6)
и с учетом (5.2) и (5.5) получаем:
 (5.7)
(5.7)
По экспериментальным данным при турбулентном истечении воды из круглого отверстия при совершенном сжатии можно считать:
a = 1,01...1,13 (Re » 104...105);
x» 0,06;
e » 0,64;
j » 0,92...0,97;
m » 0,59...0,62.
Расход жидкости и соответствующие коэффициенты истечения для некруглых отверстий при такой же площади всегда меньше из-за несовершенства их формы.
Истечение жидкости через насадки. Насадком называется короткий патрубок длиной обычно (3...5)do, присоединенный к отверстию с внешней или внутренней стороны. Применяют насадки с целью увеличить расход или изменить (увеличить, уменьшить) кинетическую энергию струи. Для увеличения пропускной способности водосбросов на дамбах, плотинах и ускорения опоражнивания емкостей обычно используют цилиндрические насадки. Конические сходящиеся и коноидальные насадки (конфузоры) применяют с целью увеличения скорости, дальнобойности и силы удара струи (гидромониторы, брандспойты, входные элементы насосов, вентиляторов, струйные усилительные элементы, расходомеры и т.п.). Конические расходящиеся насадки (диффузоры) позволяют преобразовать часть кинетической энергии потока в потенциальную, т.е. повышают давление и уменьшают скорость, что используется, например, в выходных элементах насосов и вентиляторов, в топливоподающих элементах для лучшего распыления горючей смеси.
Для расчета насадков пригодны те же закономерности, что и для малого отверстия, но численные значения коэффициентов истечения e, m, x, j имеют другие значения (табл. 5.1) и определяются экспериментально.
Существенная разница величин коэффициентов обусловлена различием условий входа, протекания и истечения жидкости.
На примере внешнего цилиндрического насадка рассмотрим особенности протекания жидкости в нем по рис. 5.2.

Рис. 5.2. Схема истечения через внешний насадок
Условия и характер течения жидкости на входе в патрубок с острой входной кромкой такие же, как и для отверстия. В сечении 1–1 струя максимально сжата, а на участке 1–2 она плавно расширяется, заполняя все сечение патрубка.
Таблица 5.1
| Вид насадка | Схема | e* | x | j | m* |
| 1.Цилиндрический внешний | 
| 0,5 | 0,82 | 0,82 | |
| 2.Цилиндрический внутренний | 
| 0,71 | 0,71 | ||
| 3.Конический сходящийся b = 13,4o | 
| 0,98 | 0,06...0,09 | 0,96 | 0,94 |
| 4.Конический расходящийся b = 7o | 
| 3...4 | 0,45 | 0,45 | |
| 5.Коноидальный | 
| 0,04 | 0,98 | 0,98 | |
| 6.Круглое отверстие | 
| 0,62...0,64 | 0,06 | 0,97 | 0,61 |
*коэффициенты e и m относятся к выходному сечению патрубка.
Между сжатой струей и стенкой насадка образуется водоворотная (вихревая) зона с пониженным давлением рвак. Это можно доказать, используя уравнение Бернулли для сечений 1–1 и 2–2. Поскольку в сечении 1–1 скоростной напор больше, чем в сечении 2–2, то для выполнения постоянства суммы скоростного и пьезометрического напоров (смысл уравнения Бернулли) напор (или давление) в сечении 1–1 должен быть меньше. При истечении в атмосферу р2 = ратм и, следовательно, р1<ратм, т.е. в сечении 1–1 создается вакуум.
С увеличением действующего напора Н и, следовательно, скорости истечения вакуум возрастает, и в критической ситуации может начаться испарение и кипение жидкости – кавитация в вихревой зоне.
Влияние вакуума на расход жидкости двоякое. С одной стороны, пониженное давление тормозит транзитную струю, т.е. возрастает коэффициент сопротивления x, но, с другой стороны, создается эффект “подсасывания” жидкости из резервуара, что в итоге ведет к значительному увеличению расхода.
Из описанной схемы истечения следует, что расход через отверстие в толстой стенке при  будет примерно на 35% больше, чем через такое же отверстие в тонкой стенке.
будет примерно на 35% больше, чем через такое же отверстие в тонкой стенке.
Эффект Коанда заключается в отклонении струи от нормальной траектории в направлении близлежащей твердой границы пространства и поясняется рис.5.3.
| Рис. 5.3. Схема, поясняющая эффект Коанда |
 Если к струе приближать твердую стенку (например пластину), то имеющийся между ними воздух частично уносится струей жидкости, т.е. в зазоре D увеличивается скоростной напор, а следовательно, понижается давление. Вследствие разности абсолютных давленийструя отклоняется в сторону стенки.
Если к струе приближать твердую стенку (например пластину), то имеющийся между ними воздух частично уносится струей жидкости, т.е. в зазоре D увеличивается скоростной напор, а следовательно, понижается давление. Вследствие разности абсолютных давленийструя отклоняется в сторону стенки.
Этот эффект часто используется в струйной технике.
Инверсией струи называется процесс плавной трансформации формы поперечного сечения струи, вытекающей из отверстий полигональной (многоугольной) формы. На рис. 5.4 это показано на примере струи из треугольного отверстия.

Рис. 5.4. Инверсия струи из треугольного отверстия
до ее разрушения
Трансформация формы струи объясняется различной скоростью входа струек жидкости по углам и граням отверстия, действием сил поверхностного натяжения, стремящихся придать струе круглую форму, и противодействующих этому инерционных сил.
Практическое применение процессу инверсии струи пока не найдено, однако вследствие своей зрелищности это явление иногда применяется в фонтанных устройствах.
5.2. Экспериментальная часть
А. Лабораторная установка
Конструкция установки (рис. 5.5) включает напорный коллектор 1 с комплектом струеформирующих головок 2, имитирующих истечение через отверстия различной формы (круглое, призматическое, треугольное и др.) и насадки (цилиндрические, конические, коноидальные и др.).
Поперечный размер коллектора на порядок больше размера отверстий, что позволяет получить совершенное сжатие струи. Необходимый напор Н в коллекторе регулируется вентилем 3 и регистрируется пьезометром 4. Траекторию и дальность полета струи можно регулировать углом a наклона коллектора относительно горизонтальной плоскости, который определяется по угломеру 5. Вода сливается по желобу 6 в бачок 7, шарнирно прикрепленный к основному баку 8. Приращение уровня в бачке определяется переносным пьезометром 9.

Рис. 5.5. Конструктивная и расчетная схема
лабораторной установки
Б. Порядок выполнения опытов
При закрытом вентиле 3 слить воду из бачка 7, ввернуть в резьбовое отверстие коллектора головку с круглым отверстием и закрепить коллектор под желаемым углом наклона a в пределах 10...70º. Измерить вылет головки  . Открыть вентиль 3 так, чтобы дальность полета струи вдоль оси Х была 30...40 см. При помощи переносного пьезометра определить приращение уровня воды в бачке 7 за время 30...120 с. Возможно измерение объема вытекшей воды непосредственным измерением при помощи отдельной наборной и мерной емкостей. Одновременно с выполнением этих замеров зафиксировать показание пьезометра 4 и определить дальность полета струи (Х) по горизонтальной шкале на баке 8. Изменять дальность полета струи при помощи вентиля 3, повторить опыты при Х »50...60 см и Х »70...80 см. Все результаты внести в табл. 5.2.
. Открыть вентиль 3 так, чтобы дальность полета струи вдоль оси Х была 30...40 см. При помощи переносного пьезометра определить приращение уровня воды в бачке 7 за время 30...120 с. Возможно измерение объема вытекшей воды непосредственным измерением при помощи отдельной наборной и мерной емкостей. Одновременно с выполнением этих замеров зафиксировать показание пьезометра 4 и определить дальность полета струи (Х) по горизонтальной шкале на баке 8. Изменять дальность полета струи при помощи вентиля 3, повторить опыты при Х »50...60 см и Х »70...80 см. Все результаты внести в табл. 5.2.
Опыты с исследуемым насадком (тип насадка задается преподавателем) проводятся аналогично, а полученные результаты сравниваются после обработки экспериментальных данных.
Эффект Коанда демонстрируется с участием преподавателя. При исследовании отверстий с полигональной формой надо визуально убедиться в существовании процесса инверсии струи.
В. Обработка экспериментальных данных
1. Определить фактическую скорость истечения струи по ее начальным (хo,yo) и конечным координатам (x,y) по формуле
 см/с.
см/с.
В соответствии со схемой (рис. 5.5):

где х – регистрируемая дальность полета струи; у = 0.
2. Вычислить действующий напор:

3. Определить теоретическую скорость истечения по формуле (5.3) и коэффициент скорости:

4. Вычислить коэффициент сопротивления x по формуле (5.4), приняв a »1,05.
5. Определить объем вытекшей воды W по измеренному приращению уровня в бачке (площадь бачка равна 411 см2) и рассчитать секундный расход:

6. Из формулы (5.2) определить площадь струи в сжатом сечении fc и коэффициент сжатия e, вычислить коэффициент расхода по формуле (5.6).
7. Рассчитать теоретический расход по формуле (5.7) и сопоставить его с фактическим по п. 5.
8. В отчете кратко описать результаты визуального наблюдения инверсии струи и эффекта Коанда.
Таблица 5.2
| Схема и геометрические параметры отверстия и заданного насадка | Круглое
отверстие
 d = l = d = l =
| Заданный насадок
d =
l =
| |||||
| № опыта | |||||||
| Угол истечения воды к горизонтали | a, град | ||||||
| Показания пьезометра | hш, см | ||||||
| Объем вытекшей воды | W, см3 | ||||||
| Время истечения | t, с | ||||||
| Дальность полета струи | X, см | ||||||
| Действующий напор | H, см | ||||||
| Фактический расход воды | Q, см3/c | ||||||
| Фактическая скорость истечения | V, см/с | ||||||
| Теоретическая скорость истечения | Vид, см/с |
Продолжение табл. 5.2
| № опыта | |||||||
| Коэффициент скорости | ji | ||||||
| jср | |||||||
| Коэффициент сопротивления | zi | ||||||
| z ср | |||||||
| Коэффициент сжатия | ei | ||||||
| eср | |||||||
| Коэффициент расхода | mi | ||||||
| mср |
Лабораторная работа № 6
Дата добавления: 2015-04-18; просмотров: 324; Мы поможем в написании вашей работы!; Нарушение авторских прав |