Модели электросопротивления аморфных сплавов

1. Дифракционная модель.

Причина необычных физических свойств аморфных металлических сплавов заключается в их структурных особенностях - отсутствии дальнего порядка. Поэтому совершенно естественно, что самые первые модели электропроводности АС основывались на том, что структура аморфного материала может быть представлена, как структура замороженной жидкости. Как следствие этого базовая модель электросопротивления АС (дифракционная модель) основана на модели Займана для одноатомных металлических расплавов.

Основные положения модели:

1. Электрическое сопротивление жидкого металла, как и любого кристаллического металла, определяется рассеянием электронов на ионах.

2. Распределение ионов в (центров рассеяния) однородно и случайно. Ионная структура может быть описана с помощью Функции Радиального Распределения, которая находится по результатам дифракционных экспериментов. С другой стороны, характер распределения атомов в пространстве определяет величину и функциональный вид структурного фактора материала Q(s).

3. Предполагается, что электроны проводимости находятся в состоянии вырожденного газа со сферической поверхностью Ферми, (т.е. рассматривается модель свободных электронов).

Для Ферми частиц, (коими являются и электроны) вырождение соответствует почти полному заполнению частицами состояний с энергией, меньшей Ферми энергией и слабому заполнению лежащих выше состояний.

Модель Друде (классическая модель газа свободных электронов для кристаллических металлов): каждый атом отдает по крайней мере один электрон электронному газу. Каждый электрон обладает кинетической энергией (3/2)кТ. Т.о. в модели Друде все электроны движутся со средней квадратичной скоростью, определяемой распределением Больцмана.

Электросопротивление рассчитывается с помощью теории псевдопотенциалов. При свободном движении электронов проводимости они рассеиваются на суммарном потенциале ионов , где V(r-r_i) потенциал взаимодействия с отдельным ионом.

Рассматривая рассеяние электронов на ионах и проводя усреднение по всему ансамблю ионов Займан получил следующее выражение для электросопротивления жидкого металла:

(*)

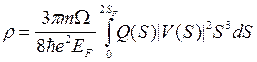гдеm - масса электрона, W - атомный объем, E_F - Энергия Ферми, Q(S) - статический структурный фактор; S — волновой вектор электронов (вектор рассеяния);; V(S) - Фурье-компонента потенциала V(r) [это есть результат интегрирования по всем радиус векторам усредненного потенциала рассеяния]; S_F волновой вектор электронов на поверхности Ферми (говоря иначе - радиус сферы Ферми в пространстве волновых векторов).

Т.о. интегрирование проводится по всей поверхности Ферми;

электросопротивление металла определяется рассеянием на псевдопотенциале иона (т.е. зависит от индивидуальных характеристик металла), а совокупное влияние других ионов выражается через структурный фактор материала.

Если рассматривать сплавы, то необходимо в выражении (*) включать парциальные структурные факторы и потенциалы ионов разного сорта. Если сплав содержит сильно рассеивающие ионы то псевдопотенциал V заменяют на более сложное выражение (вводят t-матрицу).

Наибольшим успехом модели Займана явилось простое объяснение отрицательного значения ТКС. В выражении (*) стоит куб волнового вектора S, очевидно, что при расчете этой интегральной суммы основной вклад в r будут давать значения вычисленные для S, значения которых близки к верхнему пределу интегрирования 2S_F , т.е. для максимальных значений волнового вектора.

Тогда, полагая, что S_p»2S_F из выражения (*) получаем, что температурная зависимость электросопротивления аморфных сплавовопределяется температурной зависимостью структурного фактора Q(2S_F) при значении волнового вектора равном диаметру сферы Ферми:

, где К коэффициент

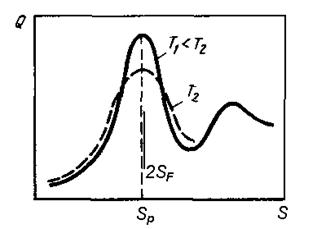
Из структурных исследований известно, что при увеличении температуры основной максимум структурного фактора уширяется, уменьшаясь по амплитуде, что обусловлено общим тепловым уменьшением степени упорядоченности ионов. Уменьшение значения Q(2S_F) с ростом температуры (при тех-же значениях S) ведет к уменьшению значений электросопротивления. Очевидно, что при этом ТКС материала - отрицательный.

В дальнейшем оказалось, что условие близости волнового вектора, соответствующего максимуму Q, к значению 2S_F (S_p»2S_F) выполняется для большого числа аморфных сплавов и это условие получило название условие Нагеля-Тауца. Это условие выполняется и для сплавов простых металлов и для сплавов металл-металлоид. Т.о. эта модель хорошо объясняет наличие отрицательного ТКС в АС.

Другим большим преимуществом дифракционной модели является возможность объяснения зависимости ТКС от состава (изменение его знака при изменении состава).

Если электроны проводимости рассматриваются как вырожденный газ со сферической поверхностью Ферми тогда

где n - плотность электронов, е - заряд электрона, R_H - коэффициент Холла.

или иначе, S_F=(3p²n_eN₀r/M_cp), где

n_e – среднее число электронов на атом, r - плотность материала, M_cp – средняя атомная масса.

Иными словами диаметр сферы Ферми зависит от концентрации электронов проводимости в материале. Соответственно, относительное положение S_p и 2S_F будет определяться концентрацией валентных электронов.

Например: для чистых переходных металлов с валентностью Z=1 значения 2S_F меньше, чем S_p. Следовательно при увеличении температуры сопротивление сплавов будет увеличиваться т.к. при данных значениях S (близких к величине 2S_F но отличающихся от S_p ) структурный фактор возрастает с ростом температуры. Это та область волновых векторов, в которой проявляется уширение главного максимума структурного фактора (см. рис). Т.о. ТКС сплавов положителен. Добавление поливалентных металлов приводит к увеличению n, повышению 2S_F, и возрастанию удельного значения электросопротивления (через возрастание величины Q(S) при приближении 2S_F к S_p ). В области составов, когда S_p»2S_F ТКС сплавов будет уже отрицательным.

В реальных металлических аморфных сплавах ситуация, конечно, намного сложнее. Помимо структурного фактора на величину электросопротивления при повышении температуры оказывает влияние и фононный спектр сплавов. Дело в том, что рассеяние на фононах (точно так же как и в кристаллических сплавах) увеличивает электросопротивление материала и если температурная зависимость структурного фактора предполагает отрицательный ТКС, а учет фононов - положительный, результат будет определяться конкуренцией двух этих процессов. Поэтому теория Займана модифицировалась с целью учета фононного спектра и учета неупругого рассеяния электронов на фононах.

Изменения касались в большей степени методов расчета структурного фактора сплавов для учета неупругого рассеяния электронов проводимости на фононах. Вместо статического структурного фактора используют динамический структурный фактор, зависящий от колебаний ионов. Кроме того учитывают уменьшение рассеяния электронов на ионах из-за колебаний последних, вводя безразмерный фактор Дебая-Валлера. В результате выражения становятся намного сложнее и более громоздкими, однако такая модифицированная теория Займана дает в ряде случаев очень хорошее количественное согласие с экспериментом.

Фактор Д-В безразмерный коэффициент W характеризующий влияние колебаний кристаллической решетки (фононов) на процессы рассеяния или излучения в кристалле без отдачи. Фактор Д-В определяет температурную зависимость вероятности процессов, при которых импульс передаётся кристаллу как целому, без изменения состояния системы фононов. Наличие тепловых колебаний крист. реш. уменьшает интенсивность процессов рассеяния: I=I₀exp(-W) I₀ интенсивность рассеяния на жёстской решётке. [Физ-я Энц-я, т.1 с.574]

где So(Q)—структурный фактор упругого рассеяния; М—масса иона; e^-2w—фактор Дебая—Валлера.

Поскольку величина коэффициента перед температурой имеет порядок не больше чем 10^-2, можно считать, что вклад фононного рассеяния в температурную зависимость электросопротивления аморфных сплавов мал. В области высоких температур фононное .рассеяние, согласно (1), дает зависимость р ~ Т. Однако изменение структурного фактора Qo(S) в (1), как и в случае жидкого металла, пропорционально Т, и если выполняется условие Q»2kp, то получается, что р ~ - Т. Следовательно, можно предположить, что при высоких температурах T> q_d знак ТКС аморфных сплавов контролируется соотношением вкладов от структурного фактора, с одной стороны, и | от фононного рассеяния, с другой.

В области промежуточных температур, T<.Q_D, фононное рассеяние, согласно (2), дает закон р~Т².

Коут и Майзель, используя модельную структуру жестких сфер двух сортов для определения Qo(S), рассчитали зависимость электросопротивления аморфных сплавов Ni—Р от температуры и химического состава и сравнили результаты расчетов с экспериментальными данными.

Как виднo, из рис. в области низких температур от Т=0 расчет дает закон Т², а в области высоких температур, при Г>0,5 Т_D - закон Т. С ростом концентрации фосфора (кривые А—Е) знак меняется < положительного на отрицательный. Все это хорошо согласуется с экспериментальными результатами.

7.2 Моделирование стадии диффузионной загонки примеси

Рассмотрим простейшую математическую модель стадии диффузионной загонки примеси. Поскольку характерная глубина проникновения примеси на стадии загонки значительно меньше не только толщины пластины, но и поперечных размеров окна в маске, пренебрежем краевыми эффектами. Будем рассматривать участки окна, достаточно удалённые от краёв маски, и считать, что условия диффузионного внедрения примеси одинаковы по всей поверхности этих участков. Тогда распределение объёмной концентрации примеси N (см^-3) будет зависеть только от расстояния x до поверхности пластины и времени t, т.е. N=N(x, t). Сам полупроводник будем считать полуограниченным телом, расположенным в области .

В простейшем случае коэффициент диффузии данной примеси в кремнии можно считать величиной, зависящей только от температуры. Как показывает эксперимент, температурная зависимость коэффициента диффузии в твёрдой фазе в широком диапазоне температур подчиняется закону Аррениуса (см. п.п. 2.2.2.2):

^, (3.2.1)

где D₀ (см² / с) – множитель с размерностью коэффициента диффузии; Е (эВ) – энергия активации диффузии; k = эВ/К – постоянная Больцмана; Т – абсолютная температура.

В соответствии со сделанными предположениями концентрация диффундирующей примеси в объеме полупроводника подчиняется уравнению

(3.2.2)

Обсудим граничные и начальные условия, которым подчиняется функция N(x,t) на стадии загонки. Благодаря интенсивному подводу примесного компонента из парогазовой смеси его концентрация непосредственно у поверхности пластины поддерживается постоянной, близкой к пределу растворимости легирующей примеси в кремнии при температуре диффузии. Поэтому граничное условие на поверхности пластины можно записать в виде:

(3.2.3)

Значение постоянной N₀ определяется, вообще говоря, сочетанием технологических факторов: температурой источника диффузанта, температурой в реакторе, расходом газа-носителя, скоростью диффузии ангидрида примесного компонента через растущий слой диоксида кремния и гидродинамической обстановкой в реакторе. Однако ведущим фактором остаётся предел растворимости примеси в кремнии при заданной температуре. Поэтому в первом приближении значение постоянной N₀ следует определять по кривым растворимости легирующих примесей в кремнии (рис. 3.2.4). При выполнении граничного условия (3.2.3) говорят, что диффузия происходит из постоянного источника (из источника неограниченной мощности).

Пусть исходная пластина не содержит примеси данного сорта. Поскольку глубина загонки всегда много меньше толщины пластины, то второе граничное и начальное условия для концентрации диффундирующей примеси будут иметь вид:

, (3.2.4)

. (3.2.5)

Решение поставленной краевой задачи для стадии диффузионной загонки из постоянного источника имеет вид:

, (3.2.6)

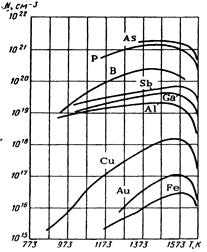
Рис. 3.2.4. Температурная зависимость растворимости различных элементов в кремнии /3, с 177/

где дополнительная функция ошибок определяется равенством:

, (3.2.7)

Определяющее соотношение для функции ошибок имеет вид:

, (3.2.8)

На рисунке 3.2.5 в качестве примера изображены концентрационные профили сурьмы в кремниевой пластине, первоначально лишенной примеси, после диффузии из постоянного источника при Т = 1260К. Время загонки: .

Дозой легирования Q принято называть количество примеси, проникшей через единицу поверхности пластины за всё время легирования t. Она может быть определена по одной из следующих формул:

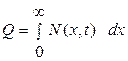, (3.2.9)

. (3.2.10)

В формуле (3.2.10) J^(N)(0,t) (см^-2с^-1) – плотность потока примесного компонента через поверхность пластины.

Найдем зависимость дозы легирования Q (см^-2) от параметров процесса загонки. Воспользуемся формулой (3.2.10). В соответствии с первым законом Фика в форме (2.2.10) и формулой (3.2.6), проекция плотности потока примесного компонента на ось ОХ вычисляется по формуле

, (1)

Вычисление производной в (1) требует вычисления производной от функции ошибок, определяемой интегралом в (3.2.8).

Рис. 3.2.5. Зависимость концентрации сурьмы, измеренной в (см^-3), от расстояния до поверхности пластины после загонки в кремний при температуре Т = 1260К. Время загонки: t₁ = 1000 c, t₂ = 2000 c, t₃ = 3000 c. Ось концентрации представлена в логарифмическом масштабе.

Как известно, производная от интеграла по переменному верхнему пределу равна подинтегральной функции. Учитывая правило вычисления производной от сложной функции, в соответствии с (1) находим:

, (2)

где . Выполняя вычисления, получаем:

(3.2.11)

Видим, что плотность потока диффундирующего компонента через поверхность пластины в процессе загонки убывает пропорционально . Подставляя (3.2.11) в (3.2.10) и выполняя интегрирование, получим формулу для вычисления дозы легирования в процессе загонки примеси путём диффузионного легирования из постоянного источника:

, (3.2.12)

Из (3.2.12) видно, что доза легирования возрастает с увеличением времени загонки по закону 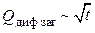. Оценим величину х_заг - характерную глубину проникновения примеси в пластину на стадии загонки. В таблице 3.2.3 приведены значения дополнительной функции ошибок при малых значениях аргумента. Данные таблицы 3.2.3 показывают, что при значениях аргумента ξ ≥ 1.2 значения дополнительной функции ошибок не превышают 0.1. Это позволяет получить оценку для характерной глубины проникновения примеси на стадии загонки из соотношения .

Таблица 3.2.3. Значения дополнительной функции ошибок при малых значениях аргумента.

	0,5		1,2	1,5
	0,48	0,16	0,09	0,05

Следовательно, толщина приповерхностного легированного слоя, получаемого в результате проведения диффузионной загонки, оценивается выражением

. (3.2.13)

Билет №7

3.Спонтанная поляризация.Условия существования спонтанной поляризации в дипольных кристаллах.Колличественная мера спонтанной поляризации.

4 Спонтанная поляризация Векторная сумма всех электронных и атомных дипольных моментов элементарной ячейки дипольного кристалла составляет ее электрический момент

(1.7)

Эту величину, характеризующую распределение электрических зарядов всей структуры кристалла, будем называть спонтанной поляризацией элементарной ячейки. Само название подчеркивает отличие спонтанной поляризации, существующей в кристаллах в отсутствие внешнего электрического поля, от индуцированной поляризации. Индуцированная поляризация состоит в возникновении дипольных моментов структурных элементов и их закономерной ориентации под действием приложенного к кристаллам внешнего электрического поля.

Для бездипольных кристаллов р_s= 0, т.е. они принципиально не могут обладать спонтанной поляризацией. Для дипольных кристаллов имеются две возможности:

а) электронные дипольные моменты скомпенсированы и отсутствуют атомные дипольные моменты, т.е. р_s = 0;

б) электронные дипольные моменты не скомпенсированы или атомные дипольные моменты не равны нулю, или отличны от нуля и те, и другие дипольные моменты, т.е. р_s ¹ 0 .

Кристаллы, имеющие отличную от нуля спонтанную поля­ризацию, должны по своей точечной симметрии принадлежать к полярным кристаллографическим классам. В этом случае кристалл рассматривается как непрерывная анизотропная среда, так как при суммировании атомных и электронных ди­польных моментов мы отвлекаемся от конкретного располо­жения атомов в структуре, сводя начало векторов дипольных моментов в одну общую точку.

Спонтанная поляризация элементарной ячейки является микроскопическим параметром структуры кристалла и не мо­жет быть непосредственно измерена в эксперименте. Для по­лучения связи спонтанной поляризации с измеряемыми в экс­перименте макроскопическими параметрами введем величину, равную векторной сумме спонтанных поляризаций элементар­ных ячеек, находящихся в единице объема кристалла

(1.8)

где N - число элементарных ячеек в единице объема кристалла.

Определенная таким образом величина называется спонтанной поляризацией единицы объема или просто спонтанной поляри­зацией. Для большинства полярных кристаллов Р_s имеет то же направление, что и р_s элементарных ячеек. В системе СИ спонтанная поляризация измеряется в [Кл/м²].