
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Лазерное распыление графита
Углеродные нанотрубки можно получить в результате термического испарения графита лазерным лучом. В качестве источника энергии может, например, служить импульсное излучение неодимового лазера [8]. Графитовый стержень-мишень диаметром 1,25 см находится внутри кварцевой трубки диаметром 2,5 см и длиной 50 см, которая, в свою очередь, помещается в нагревательную печь. Мишень, т.е. графитовый стержень, обдувается аргоном при давлении 500 Торр и облучается импульсным излучением неодимового лазера (Я = 0,532 мкм) длительностью импульса 10 не с энергией 250 тДж и частоте повторения импульсов 10 Гц. Диаметр лазерного пятна 3 или 6 мм. Распыляемый материал собирался с водоохлажденного приемника, размещаемого в нижнем по потоку конце кварцевой трубки, а также с его стенок и с нижней поверхности графитового стержня. Осадок содержал многослойные нанотрубки с числом слоев от 4 до 24 и длиной до 300 нм. Однослойных нанотрубок не наблюдалось. По мере уменьшения температуры печи качество нанотрубок ухудшалось: при 1000 °С образовывались бездефект-
ные нанотрубки, при 900 °С — богатые дефектами, а при 200 °С полное отсутствие нанотрубок. Предполагается, что нанотрубки растут в газовой фазе.

 Производство нанотрубок с использованием металлических катализаторов приводит к более высоким показателям качества и количества нанотрубок. Образцы для облучения готовятся следующим образом [9]. Смесью графита и металлического порошка заполняется форма диаметром 1,25 см. Затем форма помещается под гидравлический пресс и выдерживается при 120 °С под постоянным давлением в течение 4 — 5 часов. Спеченный образец-стержень выдерживается в течение 8 часов при 810 °С в потоке аргона. (Процесс, получивший название вулканизация.) Полученные мишени нагревались в потоке аргона до 1200 °С в течение 12 часов. Кроме того, перед каждым новым экспериментом мишень выдерживалась в потоке Аг при Т = 1200 °С в течение 2 часов. Использовались металлы при следующих концентрациях (ат. %): Со — 1,0 %; Си—0,6 %; Nb — 0,6 %; Ni — 0,6 %; Pt — 0,2 %; Co/Ni — 0,6/0,6 %; Co/Pt — 0,6/0,2 %; Со/Си — 0,6/0,5 %; Ni/Pt — 0,6/0,2 %.
Производство нанотрубок с использованием металлических катализаторов приводит к более высоким показателям качества и количества нанотрубок. Образцы для облучения готовятся следующим образом [9]. Смесью графита и металлического порошка заполняется форма диаметром 1,25 см. Затем форма помещается под гидравлический пресс и выдерживается при 120 °С под постоянным давлением в течение 4 — 5 часов. Спеченный образец-стержень выдерживается в течение 8 часов при 810 °С в потоке аргона. (Процесс, получивший название вулканизация.) Полученные мишени нагревались в потоке аргона до 1200 °С в течение 12 часов. Кроме того, перед каждым новым экспериментом мишень выдерживалась в потоке Аг при Т = 1200 °С в течение 2 часов. Использовались металлы при следующих концентрациях (ат. %): Со — 1,0 %; Си—0,6 %; Nb — 0,6 %; Ni — 0,6 %; Pt — 0,2 %; Co/Ni — 0,6/0,6 %; Co/Pt — 0,6/0,2 %; Со/Си — 0,6/0,5 %; Ni/Pt — 0,6/0,2 %.
Излучение лазера (неодим, Я = 0,532 мкм) с энергией импульса 300 тДж фокусировалось на плоскость металл-графитового композита в пятно диаметром 6 — 7 мм. Мишень находилась в камере, через которую прокачивался аргон при давлении 500 Торр. Камера помещалась в печь, с температурой 1200 °С. Продукты распыления, образующиеся в результате лазерного термического испарения мишени, уносились потоком аргона из нагретой области и осаждались на охлаждаемый водой коллектор. Собранный осадок диспергировался в метаноле с помощью ультразвука в течение 1 часа.
В электронном микроскопе, наряду с наночастицами, имеющими форму многогранников, наблюдались однослойные нанотрубки диаметром около 1 нм, выход которых возрастал при повышении температуры печи. Более высокий выход нанотрубок наблюдался в том случае, когда в качестве катализатора использовался никель.
До недавних пор считалось, что атмосфера гелия является необходимым условием образования одностенных нанотрубок в процессе лазерной абляции. Это приводило к усложнению и удорожанию экспериментов. Однако теперь метод усовершенствовали, применяют разряд не только в гелиевой, но и в водородной атмосфере, и в атмосфере азота. При этом регулируют давление, применяют катализаторы — в результате в течение нескольких часов можно получить около одного грамма черного порошка, содержащего свыше 96% одних только нанотрубок.
Например, в атмосфере азота эксперименты проводят при температуре поверхности графитовой мишени 1200 °С и давлении азота в камере - 500 Торр. Излучение второй гармоники не-одимового лазера с длительностью импульса 8 не фокусируют на поверхность мишени, обеспечивая плотность энергии - 3 Дж/см2. В графитовую мишень добавляют 1,2 ат. % примеси Ni и Со в качестве катализатора. Образующаяся в результате сажа содержит до 50% однослойных нанотрубок диаметром 1,3-1,4 нм. Часть трубок соединена в жгуты диаметром до 30 нм. Измерения, выполненные методом спектроскопии энергетических потерь электронов, показывают, что полученные нанотрубки практически не содержат азота. Выход и структурные характеристики нанотрубок аналогичны соответствующим параметрам нанотрубок, синтезированных в атмосфере гелия.
Метод химического осаждения (метод пиролиза)
Метод химического осаждения из паровой фазы заключается в разложении газообразного углеводорода, например, метана (СН4), при температуре 1100°С. При разложении газа образуются свободные атомы углерода, конденсирующиеся затем на более холодной подложке, которая может содержать разнообразные катализаторы, такие как железо. Этот процесс позволяет получать продукт непрерывно и, возможно, является наиболее предпочтительным для увеличения масштабов при промышленном производстве.
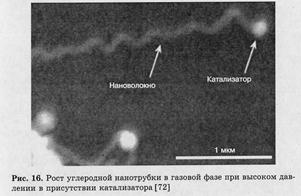
 Исследования Маринобу Эндо и его коллег из Шиншу Университета вместе с учеными из Сассекса показали, что многослойные нанотрубы можно получать пиролизом бензола C6H6 в присутствии водорода (2.22-2.24). Их метод включал ввод паров бензола и водорода в трубу керамического реактора, в которой в качестве подложки размещался центральный графитовый стержень. Температура поднималась до 1000°С и держалась на этом уровне в течение часа перед охлаждением до комнатной температуры и очищением аргоном. Осаждаемый материал был потом счищен с подложки и подвергнут «графитизирующему» тепловому воздействию при 2500-3000°С в течение примерно 10 мин. Наблюдение получающегося материала в ТЭМ показало присутствие многослойных нанотруб, практически таких же по структуре и качеству, как при их получении дуговым испарением. Казалось бы, что этот метод должен иметь потениальные возможности, хотя в настоящее время выходы пока низки.
Исследования Маринобу Эндо и его коллег из Шиншу Университета вместе с учеными из Сассекса показали, что многослойные нанотрубы можно получать пиролизом бензола C6H6 в присутствии водорода (2.22-2.24). Их метод включал ввод паров бензола и водорода в трубу керамического реактора, в которой в качестве подложки размещался центральный графитовый стержень. Температура поднималась до 1000°С и держалась на этом уровне в течение часа перед охлаждением до комнатной температуры и очищением аргоном. Осаждаемый материал был потом счищен с подложки и подвергнут «графитизирующему» тепловому воздействию при 2500-3000°С в течение примерно 10 мин. Наблюдение получающегося материала в ТЭМ показало присутствие многослойных нанотруб, практически таких же по структуре и качеству, как при их получении дуговым испарением. Казалось бы, что этот метод должен иметь потениальные возможности, хотя в настоящее время выходы пока низки.
Для получения картины роста (рис. 16) в реальном времени непосредственно внутри трансмиссионного электронного микроскопа высокого разрешения при 500 °С проводили каталитическую реакцию взаимодействия метана с закрепленными на носителе наночастицами никеля диаметром 5-20 нм. Установлено, что на поверхности частиц катализатора происходит разложение молекулы углеводорода, а образующаяся в результате мистической самосборки нанотрубка буквально свисает с мелких частиц катализатора, которые в виде своеобразной головы оказываются захвачены в точке роста нанотрубки и стимулируют ее дальнейший рост. Образующиеся при этом многослойные нанотрубки имеют примерно тот же диаметр, что и частицы катализатора. Любопытно, что рост нанотрубок сопровождается изменением формы частиц катализатора, которые из сферических становятся вытянутыми и снова сферическими. Именно на вытянутой форме как на шаблоне растет нанотрубка. В процессе реакции сохраняется кристаллическая структура частиц катализатора. Для роста нанотрубки необходимо, чтобы некоторая часть катализатора находилась в контакте с парами углеводорода; если частица катализатора оказывается внутри нанотрубки, процесс роста нанотрубки приостанавливается.
Механизм роста нанотрубок до сих пор неясен. Так как для роста однослойных трубок необходим металлический катализатор, механизм должен объяснять роль атомов кобальта или никеля. Одно из предложений, называемое «механизмом скутера», состоит в том, что атомы металлического катализатора присоединяются к оборванным связям на открытом конце трубки и обегая ее по краю, способствуют захвату атомов углерода из паровой фазы и их встраиванию в стенку трубки.
Обычно при синтезе получается смесь нанотрубок разных типов с различным характером и величиной электропроводности. Группа из IBM разработала метод отделения полупроводящих нанотрубок от металлических. Для разделения смешанные пучки нанотрубок осаждают на кремниевую подложку, а затем на эти пучки напыляют металлические электроды. Используя подложку как электрод, на него подают небольшое напряжение смещения, запирающее полупроводниковые трубки и эффективно превращающее их в изоляторы. Затем между металлическими электродами прикладывается высокое напряжение, создающее большой ток в металлических нанотрубках, что приводит к их испарению, после чего на подложке остаются только полупроводниковые нанотрубки.
Управляемый рост упорядоченных рядов углеродных нанотрубок
 На кремниевой подложке, покрытой слоем оксида кремния, удается синтезировать даже упорядоченные по заданному рисунку ряды углеродных нанотрубок [86]. С одинаковым успехом упорядочиваются и вертикальные, и горизонтальные по от-ношению к поверхности подложки трубки, причем и те, и другие можно получить даже на одной подложке. Структуры с горизонтально и вертикально упорядоченными нанотрубками необходимы для создания интегральных схем, наноэлектроме-ханических устройств, дисплеев.
На кремниевой подложке, покрытой слоем оксида кремния, удается синтезировать даже упорядоченные по заданному рисунку ряды углеродных нанотрубок [86]. С одинаковым успехом упорядочиваются и вертикальные, и горизонтальные по от-ношению к поверхности подложки трубки, причем и те, и другие можно получить даже на одной подложке. Структуры с горизонтально и вертикально упорядоченными нанотрубками необходимы для создания интегральных схем, наноэлектроме-ханических устройств, дисплеев.
Синтез осуществляется с использованием процесса химического осаждения из пара с катализатором в газовой фазе. В качестве катализатора используется смесь ксилола и ферроцена (C8H10/Fe(C5H5)2). Предварительно на подложке литографически задается рисунок, который определяет места начала роста нанотрубок и управляет направлением их роста — вертикально или горизонтально подложке. Картина роста определяется также тем, что нанотрубки растут только на оксиде кремния, но не на чисто кремниевой поверхности. Затем подложка подвергается воздействию паров катализатора при 800 °С. В результате катализатор концентрируется на подложке в канавках оксида кремния, где в дальнейшем и вырастают нанотрубки высотой до 1-2 мкм в зависимости от времени процесса (скорость роста — 10 мкм в минуту).
Для получения горизонтально направленных нанотрубок используют подложки с глубоко протравленными канавками, разделенными полосками SiO2. Рис. 18 и 19 иллюстрируют результаты роста таких структур.
Описанный процесс можно реализовать на подложках большой площади, и он полностью совместим со стандартной кремниевой технологией производства интегральных схем.

4.2 Уравнение баланса массы примесного компонента
Рассмотрим движение жидкости, в которой растворены некоторые примеси. Пусть  - массовая плотность жидкой смеси,
- массовая плотность жидкой смеси,
 - массовая плотность примеси i - го сорта,
- массовая плотность примеси i - го сорта,
 - массовая доля примеси i - ого сорта.
- массовая доля примеси i - ого сорта.
Примем, что массовые доли примесей невелики (сi << 1) и сжимаемостью жидкого раствора можно пренебречь (  ). Получим дифференциальное уравнение баланса, которому подчиняется массовая плотность примеси i - го сорта
). Получим дифференциальное уравнение баланса, которому подчиняется массовая плотность примеси i - го сорта  в движущейся жидкой смеси. Далее для краткости различительный индекс примеси i будем опускать.
в движущейся жидкой смеси. Далее для краткости различительный индекс примеси i будем опускать.
Запишем в дифференциальной форме условие баланса массы выделенного примесного компонента для бесконечно малого контрольного объема dΩ = dxdydz, неподвижного относительно лабораторной системы отсчета. Пусть
 (1)
(1)
есть изменение массы примесного компонента данного сорта в контрольном объеме dΩ за время dt. В соответствии с условием баланса оно обусловлено:
а) разностью между количеством примеси, втекающим в контрольный объем dΩ и вытекающим из него вдоль оси ОХ за время dt (рис 2.2.1)
 . (2)
. (2)
Здесь  есть проекция на ось ОХ вектора плотности массового потока выделенного примесного компонента.
есть проекция на ось ОХ вектора плотности массового потока выделенного примесного компонента.
 Рис. 2.2.1 К выводу уравнения баланса массы примесного компонента
Рис. 2.2.1 К выводу уравнения баланса массы примесного компонента
Представим величину  в виде ряда
в виде ряда
 (3)
(3)
Ограничиваясь в разложении (3) членами первого порядка малости, приведём (2) к виду
 ; (4)
; (4)
б) разностью между количеством примеси, втекающим в контрольный объем dΩ и вытекающим из него вдоль осей ОУ и ОZ за время dt. Равенства, учитывающие влияние течения примесного компонента через контрольный объём вдоль двух других осей, будут иметь вид, аналогичный (4)
 ; (5)
; (5)
 ; (6)
; (6)
в) действием источников примеси в выделенном контрольном объеме. В качестве источников примеси данного сорта могут выступать химические реакции, протекающие в многокомпонентной жидкой смеси
 . (7)
. (7)
Здесь  (
(  ) - объемная плотность мощности источников массы примесного компонента данного сорта в окрестности выбранной точки наблюдения в рассматриваемый момент времени. Очевидно, что полное изменение массы примесного компонента в контрольном объеме dΩ за время dt будет определяться суммой всех перечисленных выше вкладов:
) - объемная плотность мощности источников массы примесного компонента данного сорта в окрестности выбранной точки наблюдения в рассматриваемый момент времени. Очевидно, что полное изменение массы примесного компонента в контрольном объеме dΩ за время dt будет определяться суммой всех перечисленных выше вкладов:
 . (8)
. (8)
Из (1) с учётом (4) - (8) после сокращения на dΩ и деления на dt получаем
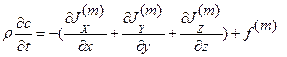 . (2.2.1)
. (2.2.1)
Это и есть искомое уравнение баланса массы примесного компонента, записанное в прямоугольной декартовой системе координат. Различительный индекс компонента опущен, но он всегда подразумевается. В векторной форме уравнение баланса массы имеет более компактный вид
 . (2.2.1.а)
. (2.2.1.а)
Отметим:
- в уравнении (2.2.1) в левой части используется локальная производная, так как контрольный объем dΩ по условию неподвижен относительно лабораторной системы отсчета;
- от уравнения неразрывности формула (2.2.1) отличается наличием слагаемого  , описывающего действие источников примесного компонента данного сорта. Если учесть, что для многокомпонентной химически реагирующей смеси
, описывающего действие источников примесного компонента данного сорта. Если учесть, что для многокомпонентной химически реагирующей смеси  ,
,  и
и  , то суммируя уравнение вида (2.2.1) по всем компонентам смеси, приходим к уравнению неразрывности.
, то суммируя уравнение вида (2.2.1) по всем компонентам смеси, приходим к уравнению неразрывности.
Перенос массы примесного компонента
в неподвижной среде. Законы Фика
Первый закон Фика
Пусть процесс молекулярной диффузии протекает в макроскопически неподвижной среде (лабораторная система отсчета движется вместе с центром масс системы). При малых градиентах температуры и малых давлениях справедлив первый закон Фика
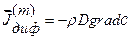 . (2.2.2)
. (2.2.2)
Здесь D (м2/с) – коэффициент молекулярной диффузии примесного компонента,  - вектор плотности массового потока примесного компонента, обусловленный механизмом молекулярной диффузии. Мы будем рассматривать первый закон Фика как закон феноменологический, являющийся обобщением данных наблюдений и экспериментов. В декартовой системе координат формула (2.2.2) принимает вид
- вектор плотности массового потока примесного компонента, обусловленный механизмом молекулярной диффузии. Мы будем рассматривать первый закон Фика как закон феноменологический, являющийся обобщением данных наблюдений и экспериментов. В декартовой системе координат формула (2.2.2) принимает вид
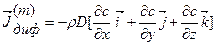 .
.
Перенос массы примесного компонента в неподвижной среде. Уравнение нестационарной диффузии
(второй закон Фика)
Обратимся к уравнению баланса массы примесного компонента (см. 2.2.1)
 . (1)
. (1)
В макроскопически неподвижной среде реализуется лишь один механизм массопереноса – молекулярная диффузия. Согласно первому закону Фика (см. 2.2.2)
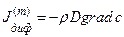 . (2)
. (2)
Считая  и
и  , после подстановки (2) в (1) получим
, после подстановки (2) в (1) получим
 (2.2.7)
(2.2.7)
или после деления на плотность раствора
 , (2.2.7а)
, (2.2.7а)
где  - локальная мощность источника массовой доли примесного компонента. Уравнение (2.2.7) есть уравнение нестационарной диффузии в неподвижной среде или второй закон Фика. Если химические реакции в системе не протекают, то
- локальная мощность источника массовой доли примесного компонента. Уравнение (2.2.7) есть уравнение нестационарной диффузии в неподвижной среде или второй закон Фика. Если химические реакции в системе не протекают, то  .
.
Различные формы записи уравнения нестационарной диффузии
Содержание примесного компонента в единице объема
смеси можно выразить различными способами:
· с помощью массовой плотности примеси ρП, (кг/м3);
· с помощью массовой доли примеси 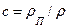 ;
;
· с помощью количества атомов или молекул примесного компонента в единице объема N (шт/м3);
· с помощью количества молей примесного компонента в единице объема n (моль/м3).
Между этими величинами имеется взаимосвязь
 , (2.2.8)
, (2.2.8)
где NA – число Авагадро, mП– масса молекулы примеси. Формула (2.2.8) позволяет переписать уравнение баланса массы и законы Фика с использованием N- и n- шкал концентраций. Например, в N – шкале уравнение баланса массы примесного компонента будет иметь вид
 . (2.2.9)
. (2.2.9)
Размерности величин, входящих в (2.2.9):  ,
, 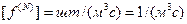 . Первый закон Фика в N – шкале будет иметь вид
. Первый закон Фика в N – шкале будет иметь вид
 . (2.2.10)
. (2.2.10)
Скалярное произведение  определяет число атомов или молекул примеси, пересекающих ежесекундно путём диффузии единичную площадку, ориентированную перпендикулярно единичному вектору
определяет число атомов или молекул примеси, пересекающих ежесекундно путём диффузии единичную площадку, ориентированную перпендикулярно единичному вектору  . Подставляя (2.2.10) в (2.2.9) и предполагая, что коэффициент диффузии не зависит от координаты, получаем уравнение нестационарной диффузии в форме
. Подставляя (2.2.10) в (2.2.9) и предполагая, что коэффициент диффузии не зависит от координаты, получаем уравнение нестационарной диффузии в форме
 . (2.2.11)
. (2.2.11)
Аналогично в n - шкале
 , (2.2.12)
, (2.2.12)
где 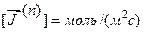 ,
,  и
и
 . (2.2.13)
. (2.2.13)
Скалярное произведение  равно числу молей примеси, пересекающих ежесекундно единичную площадку, ориентированную перпендикулярно единичному вектору
равно числу молей примеси, пересекающих ежесекундно единичную площадку, ориентированную перпендикулярно единичному вектору  . Подставляя (2.2.13) в (2.2.12) и учитывая предположение о независимости коэффициента диффузии от координаты, получаем уравнение нестационарной диффузии в форме
. Подставляя (2.2.13) в (2.2.12) и учитывая предположение о независимости коэффициента диффузии от координаты, получаем уравнение нестационарной диффузии в форме
 . (2.2.14)
. (2.2.14)
Билет 5
Билет 5.1 Возможные пути использования УНТ в наноэлектронике, энергетике и технике. Баллистическая проводимость УНТ при комнатной температуре.
4. НТ в электронике
4.1. Электрическая разводка компонентов СБИС
4.2 Полевые транзисторы с применением НТ
борьба с диоксинами
Нанотрубки для композитов
Термометр для нанообъектов
Баллистическая проводимость
Важный аспект теоретических расчетов, объясняющий большой интерес к электрическим свойствам НТ связан с тем, что электронный транспорт вдоль НТ должен быть баллистическим. Баллистический транспорт происходит тогда, когда электроны движутся вдоль проводника без какого-либо рассеяния на примесях и фононах; фактически электроны не испытывают никакого сопротивления, и в проводнике никакая энергия не диссипируется.
 Оценки показывают, что в металлическом состоянии проводимость нанотрубок очень высока. Оценочно они могут пропускать миллиард ампер на квадратный сантиметр. Медный провод выходит из строя при миллионе ампер на квадратный сантиметр из-за того, что джоулев нагрев приводит к плавлению провода. Одной из причин высокой проводимости углеродных трубок является очень малое количество дефектов, вызывающих рассеяние электронов, а следовательно и очень низкое сопротивление. Поэтому большой ток не нагревает трубку так, как он разогревает медный провод. Этому также способствует высокая теплопроводность нанотрубок. Она почти вдвое превышает теплопроводность алмаза, что означает - трубки являются очень хорошими проводниками тепла.
Оценки показывают, что в металлическом состоянии проводимость нанотрубок очень высока. Оценочно они могут пропускать миллиард ампер на квадратный сантиметр. Медный провод выходит из строя при миллионе ампер на квадратный сантиметр из-за того, что джоулев нагрев приводит к плавлению провода. Одной из причин высокой проводимости углеродных трубок является очень малое количество дефектов, вызывающих рассеяние электронов, а следовательно и очень низкое сопротивление. Поэтому большой ток не нагревает трубку так, как он разогревает медный провод. Этому также способствует высокая теплопроводность нанотрубок. Она почти вдвое превышает теплопроводность алмаза, что означает - трубки являются очень хорошими проводниками тепла.
Эксперимент
Рис. 33. Схема эксперимента для определения проводимости нанотру-бок: массив нанотрубок с торчащими из него отдельными нанотрубками погружают в жидкий металл. К системе приложено напряжение.
 Рис. 34. (А) Зависимость проводимости нанотрубки от времени для трех последовательных погружений (201-203) при возвратно-поступательном движении нанотрубки с погружением в жидкую ртуть на глубину до 2,5 мкм. (Б) Гистограмма проводимости для серии из 250 погружений. (В) Каждый скачок проводимости на Go указывает на то, что еще одна нанотрубка погрузилась в металл. (Г) Скачок проводимости на величину не кратную Go отражает наличие дефекта вблизи кончика нанотрубки
Рис. 34. (А) Зависимость проводимости нанотрубки от времени для трех последовательных погружений (201-203) при возвратно-поступательном движении нанотрубки с погружением в жидкую ртуть на глубину до 2,5 мкм. (Б) Гистограмма проводимости для серии из 250 погружений. (В) Каждый скачок проводимости на Go указывает на то, что еще одна нанотрубка погрузилась в металл. (Г) Скачок проводимости на величину не кратную Go отражает наличие дефекта вблизи кончика нанотрубки
Результаты измерений проводимости нанотрубок приведены на рис. 34. При контакте нанотрубки с жидкой ртутью проводимость в цепи скачком возрастает (рис. 34 А) на одну и ту же величину, равную кванту проводимости Go = 2e2/h = (12,9 кОм) 1. Судя по наличию плато на высоте Go, проводимость не меняется при дальнейшем погружении нанотрубки на глубину - 2 мкм и ее движении в обратном направлении до тех пор, пока остается контакт с ртутью. В интервале напряжений от 0,1 до 2 В зависимость тока от напряжения линейная с наклоном dG/dV = 0,5G0.
При обычной температуре наблюдаемое значение плотности тока (107 А-см~2) на два порядка превосходит достигнутую сейчас плотность тока в сверхпроводниках.
Таким образом, в то время как проводимость обычного провода обратно пропорциональна его длине и прямо пропорциональна поперечному сечению, в случае нанотрубки она не зависит ни от ее длины, ни от ее толщины и равна кванту проводимости — предельному значению проводимости, которое отвечает свободному переносу электронов, делокализованных по всей длине проводника.
Вычисления проводились и для многостенных нанотрубок. Оказалось, что межслоевая связь слабо влияет на электронные свойства отдельных труб. Таким образом, две коаксиальные зигзагные нанотрубы, которые как однослойные являются металлическими, образуют металлическую двустенную трубу. Полупроводящие трубы ведут себя подобным образом. Расчеты также показали, что коаксиальные трубы металл-полупроводник и полупроводник-металл сохраняют свои соответствующие характеристики при введении межслоевых взаимодействий. Поэтому идея использования двуслойных нанотруб как изолированных нанопроводов, по крайней мере теоретически, представляется верной.
Прямые измерения электрического сопротивления НТ достаточно сложны вследствие малого диаметра НТ (5-15 нм). Можно привести пару методов, которыми пользуются для измерения электрических свойств НТ
1. Сначала происходит осаждение нанотруб на оксидированную кремниевую пластину, а затем - покрытие этого депозита слоем золота, в котором позже была сформированы щели. Это способствовало выявлению многих одиноких нанотруб в открытом районе, как показано на рис. 4.12. Отдельные нанотрубы можно было обнаружить с помощью атомно-силовой микроскопии, а измерения проводимости на трубах провести, используя острие консольного устройства (кантиливера). Преимущество этого метода заключается в том, что измерения сопротивления могут быть проделаны в нескольких точках данной трубы, исключая, таким образом, контактное сопротивление.
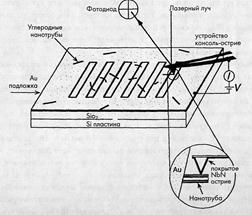
Рис. 4.12. Устройство для измерения сопротивлений отдельных нанотруб, используемое Либером и др. (4.36).
2. В другом методе трубы осаждались на оксидированную поверхность кремния между золотыми накладками. Для наблюдения за подпираемыми нано-трубами использовался микроскоп с фокусированным ионным пучком, и, когда обнаруживалась подходящая труба, напылялись четыре вольфрамовых проводка шириной 80 нм для получения устройства, подобно показанному на рис. 4.13. Затем вольфрамовые провода могли быть подсоеденены к золотым накладкам, чтобы было возможно проделать четырехзондовые измерения сопротивления. Расстояние между контактами на таких трубах было в диапазоне 0.3-1.0 мкм. Для измерения температурного влияния на сопротивление образцы накладывались на криостат.
 Рис. 4.13. Изображение четырех вольфрамовых проводков, соединенных с отдельной нанотрубой — из работы Эббесена и др. (4.37). Каждый вольфрамовый проводок имеет ширину 80 нм.
Рис. 4.13. Изображение четырех вольфрамовых проводков, соединенных с отдельной нанотрубой — из работы Эббесена и др. (4.37). Каждый вольфрамовый проводок имеет ширину 80 нм.
Разброс получаемых значений очень велик, однако можно смело утверждать, что удельное сопротивление НТ падает с увеличением диаметра.
Другим важным результатом является то, что в ряде измерений было показано, НТ имеют значения удельного электросопротивления ~ 0,05 мкм×м, т.е. при комнатной температуре уд сопр НТ может быть меньше, чем у дельное сопротивление в плоскости грнаитп.
5.2 Перенос массы примесного компонента в движущейся жидкости
1 Массовый поток примесного компонента
в движущейся среде
Конвективный перенос – это перенос чего-либо потоком движущейся жидкости. Например, река переносит опавшие в воду листья. Совместный перенос примеси диффузией и потоком движущейся жидкости называют конвективной диффузией. При этом вектор полной плотности массового потока примеси равен векторной сумме вида
 . (2.2.15)
. (2.2.15)
Обсудим физический смысл величин, входящих в это равенство:
 - массовая плотность потока примесного компонента, определяемая для контрольной площадки, неподвижной относительно лабораторной системы отсчета, и обусловленная всеми механизмами массопереноса (полная массовая плотность потока примесного компонента в ЛСО);
- массовая плотность потока примесного компонента, определяемая для контрольной площадки, неподвижной относительно лабораторной системы отсчета, и обусловленная всеми механизмами массопереноса (полная массовая плотность потока примесного компонента в ЛСО);
 - массовая плотность диффузионного потока примесного компонента. Скалярное произведение
- массовая плотность диффузионного потока примесного компонента. Скалярное произведение  определяет величину массовой плотности потока через контрольную площадку с нормалью
определяет величину массовой плотности потока через контрольную площадку с нормалью  в системе отсчета, движущейся относительно ЛСО со скоростью
в системе отсчета, движущейся относительно ЛСО со скоростью  вместе с центром масс выделенной частицы жидкости (то есть в системе отсчета, где выделенная частица жидкости покоится как целое);
вместе с центром масс выделенной частицы жидкости (то есть в системе отсчета, где выделенная частица жидкости покоится как целое);
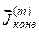 - массовая плотность потока, определяемая для контрольной площадки, неподвижной относительно лабораторной системы отсчета, но в условиях когда
- массовая плотность потока, определяемая для контрольной площадки, неподвижной относительно лабораторной системы отсчета, но в условиях когда  = 0. Иначе говоря, на период определения
= 0. Иначе говоря, на период определения 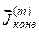 все молекулы примесного компонента «замирают» относительно своего ближайшего окружения.
все молекулы примесного компонента «замирают» относительно своего ближайшего окружения.
В выбранной точке наблюдения векторы  и
и 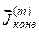 могут быть ориентированы противоположно, и один вид массопереноса ослабляет другой, а могут быть и сонаправлены. Тогда оба механизма переноса «помогают» друг другу.
могут быть ориентированы противоположно, и один вид массопереноса ослабляет другой, а могут быть и сонаправлены. Тогда оба механизма переноса «помогают» друг другу.
Пример: капля чернил в потоке речной воды. На левой стороне капли частицы чернила движутся относительно берега чуть медленнее, чем на правой стороне капли.
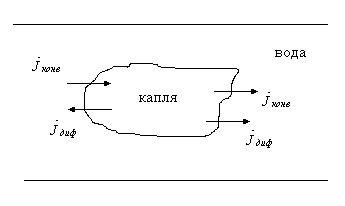
Массовая плотность конвективного потока примесного компонента выражается формулой
 . (2.2.16)
. (2.2.16)
Чтобы убедиться в этом рассмотрим рисунок 2.2.2, из которого видно, что величина массовой плотности потока через контрольную площадку  , перпендикулярную скорости потока жидкости, будет выражаться формулой
, перпендикулярную скорости потока жидкости, будет выражаться формулой
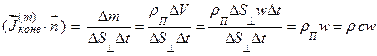 .
.

Рис. 2.2.2 – К определению массовой плотности конвективного потока
Здесь ∆m = ρП∆V =  w∆t– масса примеси, переносимая потоком через площадку
w∆t– масса примеси, переносимая потоком через площадку  за время ∆t.
за время ∆t.
С учетом ( 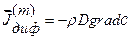 ) и (2.2.16) выражение (
) и (2.2.16) выражение (  ) для полной плотности массового потока примесного компонента принимает вид
) для полной плотности массового потока примесного компонента принимает вид
 . (2.2.17)
. (2.2.17)
2 Уравнение конвективной диффузии
Конвективная диффузия – это перенос примесного компонента в движущейся жидкости, когда имеют место оба механизма массопереноса - диффузия и конвекция. Нас будет интересовать уравнение, которому подчиняется массовая доля примесного компонента в случае конвективной диффузии.
Воспользуемся уравнением баланса примесного компонента (2.2.1)
 (1)
(1)
и выражением (2.2.17) для полной плотности массового потока примесного компонента
 . (2)
. (2)
Примем:
·  , то есть сжимаемостью среды можно пренебречь;
, то есть сжимаемостью среды можно пренебречь;
·  , то есть поток изотермический и с малым содержанием примеси.
, то есть поток изотермический и с малым содержанием примеси.
Подставим (2) в (1) и выполним необходимые преобразования.
 . (3)
. (3)
Преобразуем выражение  , учитывая, что для несжимаемой жидкости согласно уравнению неразрывности
, учитывая, что для несжимаемой жидкости согласно уравнению неразрывности
 . (4)
. (4)
Согласно известной формуле векторного анализа находим
 . (5)
. (5)
С учётом (5) формулу (3) можно переписать в виде
 . (6)
. (6)
Перенося второе слагаемое правой части выражения (6) в левую его часть и вынося за скобку  , получим
, получим
 . (2.2.18)
. (2.2.18)
Выражение в скобках в левой части (2.2.18) есть полная производная массовой доли примеси по времени. Это позволяет переписать последнее уравнение в виде
 . (2.2.18а)
. (2.2.18а)
При  уравнение (2.2.18), как и следовало ожидать, переходит в уравнение нестационарной диффузии в неподвижной среде (
уравнение (2.2.18), как и следовало ожидать, переходит в уравнение нестационарной диффузии в неподвижной среде (  ). Повторив рассуждения подпункта 2.2.2.4, легко получить выражения для уравнения конвективной диффузии в N – и n – шкалах концентрации примесного компонента. Эти вычисления рекомендуется проделать самостоятельно.
). Повторив рассуждения подпункта 2.2.2.4, легко получить выражения для уравнения конвективной диффузии в N – и n – шкалах концентрации примесного компонента. Эти вычисления рекомендуется проделать самостоятельно.
Отметим: поскольку (2.2.18) включает  , то уравнение конвективной диффузии следует рассматривать либо совместно с уравнением движения жидкости, либо поле скоростей движущейся жидкости должно быть задано.
, то уравнение конвективной диффузии следует рассматривать либо совместно с уравнением движения жидкости, либо поле скоростей движущейся жидкости должно быть задано.
Билет 6
Билет 6.1 Эмиссионные свойства УНТ, полевая эмиссия, перспективы использования и механизмы эмиссии.
Эмиссионные свойства нанотрубок
Источники электронов широко распространены как в научных исследованиях, так и в промышленности, где используется, главным образом, термоэлектронная эмиссия, когда электроны испускаются из нагретого до высоких температур источника под действием достаточно высоких напряжений (сотни и десятки кВ). В исследовательской практике требуются источники электронов с высокой яркостью и монохроматичностью. В последние годы 20 столетия появились работы [1, 2] где показано, что в качестве источников эмиссии можно использовать одиночные углеродные нанотрубки, которые могут быть источниками электронов с хорошей монохроматичностью и высокой разрешающей способностью.
В промышленности намечены грандиозные планы возможного использования углеродных нанотрубок в качестве материала для катодных эмиссионных источников в лучевых трубках (например, для гигантских дисплеев), а также для плоских дисплейных экранов. Такие устройства на основе УНТ демонстрировались уже в 1998 г. в виде катодной лучевой трубки и дисплея размером 32 х 32 пикселя.
Электронные источники становятся вездесущими и необходимыми в нашем индустриальном обществе. Центральная роль принадлежит им в информационной среде. Многократно объявлялось, что обычные катодно-лучевые трубки будут вытеснены плазменными или жидкокристаллическими дисплеями. Однако предсказания не сбылись: электронно-полевые эмиттеры стали более привлекательными после того как совсем недавно были разработаны дешевые и прочные материалы с высокими значениями полевой эмиссии электронов. К таким материалам относится, прежде всего, молибден в виде лезвий и тонких проволочек. Каков должен быть идеальный полевой эмиттер с точки зрения максимального практического использования? Рабочая часть эмиттера должна быть очень длинной и тонкой, сделана из хорошо проводящего материала с высокой механической прочностью, твердостью, быть дешевой и технологичной. Не трудно вообразить технологические трудности получения тонкой проволочки молибдена (менее 1 мкм).
Воображение рисует также плоские двумерные листы графита с планарным расположением углеродных атомов в виде гексагональных решеток и скатанных в виде цилиндра. Вы должны получить очень длинные и очень тонкие цилиндрической формы нити. Они должны обладать свойствами графита, но быть упругими, сгибаться и быть очень прочными. Ансамбль вставленных друг в друга цилиндриков наподобие русской матрешки с закрытой крышкой наверху – вот новый эмиссионный материал, который почти идеален для создания полевых эмиттеров.
Способность УНТ быть в качестве полевых эмиттеров широко освещалась, начиная с первых статей и вплоть до 1995 г., в которых говорилось об экстремально низком поле, которое необходимо для возбуждения электронов и реализации высоких плотностей тока эмиссии. Начиная с 1998 г. перспективы использования нанотрубок в качестве приборов полевой эмиссии электронов значительно усилились во всем мире. Был представлен первый дисплей со световыми элементами.
Дата добавления: 2015-04-18; просмотров: 516; Мы поможем в написании вашей работы!; Нарушение авторских прав |