Интеркалированные соединения фуллеритов

Существенные достижения в молекулярной и твердотельной химии привели к синтезу различных соединений С₆₀ с другими элементами. Как только было обнаружено, что молекулы С_т при образовании твердого тела связаны между собой ван-дер-вааль-совскими силами, сразу же возникла мысль использовать это свойство для образования соединений, в том числе таких, которые называются интеркалированными соединениями (соединения с внедренными атомами в кристаллической решетке фуллерита). В интеркалированных соединениях большие тетраэдри-ческие и октаэдрические пустоты в кристалле с ГЦК решеткой образуют слоистые галереи. В то время как основная структура остается неизменной (рис. 1.19 а), металлические свойства достигаются тогда, когда заполняется половина зоны за счет добавления трех электронов на молекулу и образуется вторая псевдоэлектронная система. Металлические свойства возникают при внедрении одновалентных ионов во все три полости твердого С₆₀. Соединения такого типа называют фуллеридами.

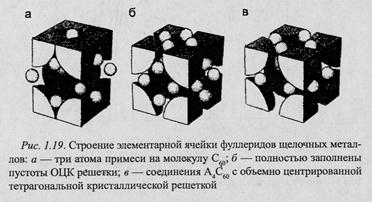
Получение таких соединений сразу же привело к открытию первых сверхпроводников на основе фуллеренов типа М_хС₆₀(М = К, Rb).

Первоначальные результаты по легированию фуллерита щелочными металлами предполагали, что легирование достигает предельного значения при х = 3. Измерения электрического сопротивления в процессе напыления металла на фуллерит показали, что по мере увеличения концентрации металла до х = 3 сопротивление уменьшается до минимальных значений, а затем по мере увеличения х сопротивление растет. Элементный анализ легированного до насыщения К и Cs фуллерита показал, что в пределе образуется композиция М₆С₆₀. Однако внедрение атомов при концентрациях х > 3 требует, чтобы сверхрешетка фуллерита преобразовалась в симметрию, отличную от ГЦК, поскольку необходимо иметь более чем три места внедрения на одну молекулу.

Первые прямые структурные доказательства были получены при использовании легированных до насыщения соединений М₆С₆₀ (М = К, Rb, Cs) [45]. Оказалось, что легирование фуллерита К, Rb, Cs до насыщения сопровождается перестройкой ГЦК решетки в ОЦК с неплотной упаковкой. На рис. 1.20 показана одна из граней такого куба. Согласно схеме, 12 атомов М на ячейку представлены в виде четырех атомов, расположенных, как в решетке алмаза, в эквивалентных положениях. Каждая молекула С₆₀ находится в окружении 24 атомов М, и каждый из этих атомов обусловливает тетрагональность четырех молекул С . Самые короткие расстояния между центрами молекул С₆₀ равны 0,979 и 1,021 нм при легировании калием и цезием соответственно. Отметим, что в нелегированной ГЦК фазе фуллери-та расстояние между ближайшими соседними молекулами С₆₀ равно 1,002 нм. Расстояния между ближайшими соседними атомами С - Cs находятся в интервале 0,338 — 0,370 нм, что сравнимо с величиной, равной 0,320 нм, как суммы ван-дер-вааль-совского радиуса атома углерода и ионного радиуса цезия. Расстояния между атомами Cs — Cs равны 0,415 нм, что значительно больше, чем ионный диаметр, равный 0,334 нм. Таким образом, при легировании фуллерита щелочными металлами получены стехиометрическая ГЦК фаза фуллерида типа М_хС₆₀ (х = = 3), стехиометрические объемно центрированные тетрагональные фазы при х = 4 и х = 6. Первая из них оказалась сверхпроводником. Исследования электрических и других свойств последних двух фаз продолжаются.

Широко известно, что свойства полупроводников можно существенным образом изменять путем их допирования. Допант может либо отдавать свои электроны в зону проводимости полупроводника (допант я-типа), либо забирать электроны из валентной зоны полупроводника (допант р-типа). При обработке фуллерита С₆₀ парами щелочных металлов происходит его допирование по n-типу, электрон щелочного металла попадает в зону проводимости, образованную t_1u-состояниями.

На рис. 1.3 представлены фотоэмиссионные спектры образцов фуллерита С₆₀, допированного калием, т. е К_хС₆о (рисунок взят из [19]). Видно, что при допировании вблизи уровня Ферми (Е_ь = 0) появляется новая полоса, интенсивность которой растет с увеличением концентрации допанта х. Емкость валентной зоны, образованной t_1u -состояниями, ограничена 6-ю электронами (в расчете на одну молекулу фуллерена). Поэтому при 0 < х < 3 проводимость образца растет с увеличением х, а при х = 6 зона проводимости оказывается заполненной полностью и свойства образца зависят от того, какая структура следующей свободной зоны, которая образуется t_lg МО состояниями.

При х = 3 зона проводимости заполнена наполовину. Именно в этом случае, как уже сообщалось, образец приобретает способность переходить в сверхпроводящее состояние при 19 К.

На рис. 1.22 представлена температурная зависимость удельного электрического сопротивления пленки К₃С_6О толщиной 160 нм [46].

Вблизи Тс, р = 3×10^-3 Ом×см, что примерно на восемь порядков ниже соответствующих значений (~ 10⁵ Ом×см) кристаллического С₆₀.

При изучении физических свойств соединений М_хС₆₀ наибольшее внимание уделялось сверхпроводящей фазе М₃С₆₀. Обнаружено, что возрастание температуры перехода в сверхпроводящее состояние Т связано с увеличением размера атома щелочного металла. Эта закономерность приводит к почти линейной зависимости между Т. и параметром а ГЦК решетки (рис. 1.21). Чтобы объяснить полученные экспериментальные данные, нужно сделать предположение о том, что имеется слабая связь в соответствии с теорией Бардина — Купера — Шриффера (БКШ теория) и что Т. зависит только от перекрытия ближайших молекул С₆₀. При этом, однако, совершенно неясны роль и влияние легирующих элементов.

Установлено, что различные щелочные металлы в соединениях типа М₃С₆₀ подчиняются правилу спаривания электронов с участием в этом процессе фононов щелочных ионов. Также установлено, что переход изолятор — металл в легированном щелочными металлами твердом фуллерите обусловлен переходом электронов из основного состояния на более высокий уровень. Можно утверждать: соединения типа М^С^ являются молекулярными металлами для некоторых концентраций х, что объясняется большим сродством электронов С^ и низким редукционным потенциалом.

Переход в сверхпроводящее состояние наблюдается вблизи 20 К. Обработка данных, представленных на рис. 1.21, позволяет получить некоторые характеристики фуллеридов. Считая, что в соединении К^С^ на каждую молекулу приходится по три электрона в зоне проводимости и пользуясь классическим выражением

где х — характерное время рассеяния электрона, тип — масса и концентрация электронов соответственно, получим х = = 3 • 10~¹⁶ с. Относительно высокое сопротивление пленок ЬЦС^ авторы [46] связывают с мелкозернистой структурой фуллерида (d = 6—8 нм), что приводит к заниженным значениям времени рассеяния электрона.

Вскоре было установлено, что сверхпроводящими свойствами обладают не только соединения К₃С₆₀, Rb₃C₆₀, но и XY₂C₆₀, где X и Y — атомы щелочных металлов. В табл. 1.2 приведены значения Тс., параметра а и доля ГЦК структуры в сверхпроводящих соединениях Х₃С₆₀ и XY₂C₆₀ [47].

Зависимость Г, фуллеридов от величины обратной плотности электронных состояний на уровне Ферми N(E_F) приведена на \ рис. 1.23 [48]. Отчетливо видна корреляция между а и 7\ Линейный характер зависимости T_c(N(E_F)) указывает на фононный механизм сверхпроводимости в фуллеридах. Согласно модельным представлениям БКШ теории, Г. выражается через параметры сверхпроводящего материала следующим образом:

Линейная зависимость Тс от плотности електр-х состна уровне Ферми (рис 1,23) свид о том, что Сверхпроводимость фуллеридов обусловлена тем-же механизмом, что и у металлов, т.е. работает теория БКШ (Бардина — Купера — Шриффера) – происходит образование Куперовских пар при обмене электронов фононами.

Тс = w×exp[-V×N(E_F)].

где со. — энергия фононов, участвующих в образовании электронных пар при возникновении сверхпроводимости; V — константа, характеризующая энергию электрон-фононного взаимодействия, приводящего к спариванию электронов. Линейный характер зависимости, представленной на рис. 1.23, согласуется с выражением (1.6) при условии, что энергия фононов со_ф= 300 К, а V = 0,03 эВ и не зависит от сорта легирующих атомов. Экспериментальные факты и модельные представления указывают на определяющий вклад внутримолекулярных колебаний С₆₀ в механизме спаривания электронов, ответственном за сверхпроводимость.

2.2.Химические равновесия.

1.7.1.Особенности изменения состава системы при химических превращениях.

При определённых условиях в смеси различных веществ может протекать процесс, при котором количество одних веществ в системе уменьшается, а других увеличивается. При этом может происходить и образование новых химических веществ, не присутствовавших в исходной смеси. Такой процесс называют химическим превращением или химической реакцией. При химических превращениях вещества реагируют друг с другом в количественных соотношениях, определяемых уравнением реакции

. (1.7.1)

Здесь А_i – химические символы участников реакции (реактантов), ν_i – соответствующие стехиометрические коэффициенты, которые для исходных веществ считаются отрицательными, а для продуктов реакции отрицательными. Стехиометрическое уравнение (1.7.1) не только описывает качественный характер химического превращения, но и является уравнением материального баланса по всем атомам, образующим молекулы реактантов. Выбор стехиометрических коэффициентов данной химической реакции неоднозначен: умножение всех коэффициентов на один и тот же множитель не нарушает условий материального баланса атомов, образующих молекулы реактантов. Чаще всего выбирают целочисленные значения стехиометрических коэффициентов, не имеющие общего целочисленного делителя (не считая ±1).

Пусть dn_i - изменение количества молей i – го вещества в ходе реакции. В соответствии со стехиометрическим уравнением (1.7.1) отношения

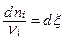(1.7.2)

Одинаковы для всех реактантов, поскольку определяют количество (молей) отдельных молекулярных актов реакции. Положительную величину ξ называют по разному:

• мерой реакции;
• глубиной реакции;
• координатой реакции;
• числом пробегов реакции и т.п.

и измеряют обычно в молях. Текущее значение количества молей каждого реактанта определяется глубиной реакции согласно формуле

, (1.7.3)

где n_oi – количество молей i – го вещества в исходной смеси.

1.7.2.Условия химического равновесия.

Химическая реакция в зависимости от условий может протекать как в прямом, так и в обратном направлении, т.е. является обратимой с химической точки зрения. Направление химического процесса определяется концентрацией реактантов, температурой и давлением. Самопроизвольно реакция протекает до тех пор, пока не будет достигнуто состояние химического равновесия между реагирующими веществами, при котором состав смеси при неизменных внешних условиях не будет изменяться с течением времени.

Условие химического равновесия можно получить, используя уравнение равновесия сложной системы в изобарно-изотермических условиях (1.5.?)

(1.7.4)

совместно с условием перераспределения масс реактантов при химических превращениях, определяемым стехиометрическим уравнением реакции. В соответствии с (1.7.2) изменения чисел молей реактантов в ходе реакции

. (1.7.5)

Подставляя (1.7.5) в (1.7.4), после сокращения на dξ ≠ 0 получаем условие химического равновесия

(1.7.6)

Число таких уравнений в условиях химического равновесия в многокомпонентной системе равно числу химических реакций, которые способны протекать в ней одновременно.

1.7.3.Константа равновесия химической реакции. Закон действующих масс.

Рассмотрим термодинамическую систему, в которой протекают химические превращения в условиях постоянства температуры и давления. Запишем стехиометрическое уравнение некоторой химической реакции в виде

(1.7.7)

где А_i – химические символы участников реакции (реактантов); ν_i - соответствующие стехиометрические коэффициенты. Суммирование проводим по всем компонентам системы, участвующим в рассматриваемой реакции.

В состоянии химического равновесия при постоянных значениях температуры и давления химические потенциалы компонентов m_i должны удовлетворять условию (1.7.6)

.

Для химических реакций, протекающих в газовой фазе при умеренных температурах и давлениях, можно полагать, что все реактанты подчиняются уравнению состояния идеального газа.

В смеси идеальных газов химический потенциал i-го компонента определяется выражением (1.5.19)

(1.7.8)

Здесь P_i – парциальное давление i-того компонента, -химический потенциал газа i-го сорта в стандартном состоянии при температуре реакции, Р⁰ – давление в состоянии, принимаемом за стандартное. Стандартное давление удобно принять одинаковым для всех компонент смеси и равным одной атмосфере. Используя (1.7.8), условие химического равновесия (1.7.6) можно записать в виде

, (1.7.9)

или после преобразования

(1.7.10)

Здесь и далее индекс «равн» означает, что парциальные давления компонентов смеси относятся к состоянию равновесия. Определим константу газофазной химической реакции К_Р соотношением

(1.7.11)

где индекс «р» указывает на то, что константа равновесия образована произведением парциальных давлений компонент в состоянии химического равновесия. Тогда уравнение (1.7.10) можно переписать в виде

(1.7.12)

Это уравнение принято называть законом действующих масс. При выбранных стандартных состояниях реактантов его правая часть зависит только от температуры и не зависит ни от суммарного давления, ни от состава исходной смеси, ни от наличия в системе инертных газов. Величину

, (1.7.13)

стоящую в числителе правой части (1.7.12), называют стандартным мольным изменением энергии Гиббса в ходе реакции, или кратко – стандартной энергией Гиббса реакции.

До сих пор мы полагали, что все реактанты находятся в газообразном состоянии. Рассмотрим теперь случай, когда некоторые вещества, участвующие в реакции, присутствуют как в парогазовой, так и в конденсированной фазах. Для простоты предположим, что имеется лишь одна конденсированная фаза, содержащая чистый компонент. Именно так и происходит при водородном восстановлении кремния. Помимо химического равновесия в такой системе имеет место и фазовое равновесие конденсированная фаза - пар конденсирующегося компонента, вследствие чего парциальное давление пара конденсирующегося компонента совпадает с давлением его насыщенного пара при температуре реакции. Оно не зависит от парциальных давления других участников реакции и остаётся постоянным до тех пор, пока будет существовать конденсированная фаза. Если при этом окажется, что давление пара конденсирующегося компонента достаточно мало, то его можно не включать в число учитываемых компонент паровой фазы.

Можно показать, что закон действующих масс и в этом случае может быть представлен формулой (1.7.12). Однако будут два существенных отличия. Во-первых, в выражении (1.7.11) для константы равновесия гетерогенной химической реакции будут фигурировать равновесные парциальные давления только неконденсирующихся компонент. Во-вторых, для компонента, находящегося как в паровой, так и в конденсированной фазах, в выражении для стандартной энергии Гиббса реакции будет фигурировать химический потенциал чистого конденсированного компонента в его стандартном состоянии при температуре реакции.

Билет 3

Билет 3.1 Эндоэдральные структуры фуллеренов

Одним из интересных направлений в физике фуллеренов является изучение так называемых эндоэдралъных структур или эндоэдральных соединений, когда внутреннюю полость молекулы фуллерена заполняет атом (или несколько атомов) другого элемента. В этом случае атом какого-либо элемента как бы закрыт сплошной оболочкой, состоящей из атомов углерода. Если в молекулу фуллерена вводятся атомы металла, то такие эндоэдральные комплексы и называются металлфуллеренами, они обозначаются как М_n@С_m, где М — атом металла, находящийся во внутренней полости фуллерена @, содержащего m углеродных атомов, n – число атомов металла в фуллерене.

n = 1, 2, 3 m = 60, 70, 72, 74, …100.

Томы которые удалось инкапсулировать составляют большую часть Период Системы :

Ca, Sr, Ba, Li, B, N, K, Na, Sc, Rb, La, Y,

Ce, Pr, Nd, Sm, Eu, Gd, Dy, Ho, Er, Yb,

Особенность электронной структуры эндоэдральных металлофуллеренов обусловлена передачей валентных электронов металла фуллереновой оболочке, поэтому внутри фуллеренового аниона находится положительный ион. Можно говорить о возникновении своеобразных комплексов.

Например: La₂³⁺@C₈₂^6- , Y₂³⁺@C₈₂^6-.

Ион металла расположен не в центре фуллерена, а смещен….След-но у металлфуллерена возникает дипольный момент. В эндометаллофуллеренах газокинетический размер инкапсулированного атома (иона) значительно меньше внутреннего размера фуллереновой оболочки, поэтому ион металла смещен относительно геометрического центра молекулы. Это определяет наличие у таких молекул постоянного дипольного момента (для молекулы Y@C₈₂ - 2,5 D, для La@C₈₂ - 3-4 D). Из-за возможности ориентации таких молекул в кристалле и возникновения постоянной поляризуемости такие кристаллы должны обладать сегнетоэлектрическими свойствами и могут найти интересные применения в электронных устройствах

Свойства эндометаллофуллеренов зависят от валентности внедренного иона. Так, эндоэдральные фуллерены, содержащие двухзарядный ион металлов второй группы, диамагнитны. Напротив, эндоэдральные фуллерены, содержащие металл третьей группы, обладают парамагнитными свойствами, поскольку инкапсулированный трехзарядный ион металла передает фуллерену три электрона.

Для получения металлфуллеренов используются различные методы. Существует два глобальных подхода:

1 - в процессе образования фуллеренов, когда часть атомов или молекул, присутствующих в зоне синтеза, оказывается внутри молекул фуллерена;

2 - внедрением атомов или молекул внутрь углеродного каркаса уже готовых молекул фуллерена [41].

Для синтеза эндофуллеренов первым методом можно успешно применять описанные установки для синтеза фуллеренов.

Наиболее простой способ введения металлического пара в зону синтеза фуллеренов основан на использовании испаряемой мишени, изготовленной из графита с добавкой небольшого количества порошка металла или его соединения (оксида, карбида, соли) [41-50].

В первых работах синтез эндометаллофуллеренов осуществляли воздействием импульсов сфокусированного лазерного излучения с длиной волны 532 нм, длительностью 5 не и энергией 30^40 мДж на пропитанную LaCl₃ графитовую поверхность [42]. Образующийся при этом углеродный пар, содержащий также примесь паров лантана, уносился потоком гелия, и по мере остывания атомов углерода происходила конденсация, сопровождаемая образованием кластеров углерода. Полученный таким образом поток кластеров направлялся в камеру масс-спектрометра. Продукты термического испарения материала мишени наряду с полыми фуллеренами С₆₀, С₇о и другими также содержали эндоэдральные фуллерены La@C₆₀ и Lа₂@ C₆₀, о чем свидетельствовал анализ масс-спектров.

В [43] синтез эндоэдральных фуллеренов проводили лазерным облучением в атмосфере гелия композитного материала, полученного прессованием La₂O₃ графитового порошка и смолы. Как показали результаты масс-спектрометрического анализа, в продуктах синтеза наряду с полыми фуллеренами присутствуют также эндоэдральные соединения типа La@C_2n, где п > 30.

Существенно более высокими показателями по выходу эндофуллеренов характеризуется электродуговой метод испарения графитметаллических композиций. В этом методе используют традиционные установки электродугового испарения графита в атмосфере гелия, когда в зону образования фуллеренов добавляется некоторое количество паров металла. При этом выход эндоэдральных металлофуллеренов достигает нескольких процентов [44].

В [45] для изготовления анода в графитовом стержне длиной 100 мм и диаметром 6 мм высверливали отверстие длиной 70 мм и диаметром 4 мм, которое заполнялось смесью порошка La₂О₃ и аморфного графита. Доля лантана в материале анода составляла 1 % (ат.). Для упрочнения материала электроды подвергали термической обработке в вакууме при температуре 1800 °С в течение 3 часов Катодом служил чистый графитовый стержень. Дуга горела в атмосфере гелия (давление 80 Торр) при токе 200 А. Образующийся катодный дпозит «дожигался» в результате смены полярно сти электродов с целью увеличения выхода эндофуллеренов. Эндофуллерены экстрагировались из сажи с помощью толуола или пиридина подвысоким давлением и при высокой температуре в течение 5 часов. Выход пиридинового экстракта составил 0,6 % от массы сажи. Полученные толуольный и пиридиновый экстракты, по данным масс-спектрометрии, представляли собой смесь полых фуллеренов и эндофуллеренов. Содержание эндофуллеренов в пиридиновом экстракте достигало ~ 75 %.

В [46] было показано, что выход экстрактов, содержащих смесь полых фуллеренов и эндометаллофуллеренов, может достигать 3,2 % от массы сажи. Композитные электроды были приготовлены по описанной методике, только вместо оксида металла авторами был использован сплав М№₂ (M=Y, La). Электроды испаряли в электрической дуге при следующих параметрах: давление гелия - 720 Торр, ток дуги - 50 А. Сажу экстрагировали сероуглеродом в аппарате Сокслета. Масс-спектрометрический анализ полученного экстракта показал (рис. 2.12), что в нем содержатся полые фуллерены и эндометаллофуллерены. Выход эндофуллеренов - ~ 1,5 % от массы сажи.

Анализ имеющихся в литературе методик синтеза эндометаллофуллеренов, например в [47-57], свидетельствует, что электродуговой метод синтеза является наиболее эффективным способом получения эндометаллофуллеренов в макроколичествах.

Синтез эндоэдральных фуллеренов внедрением атомов или молекул внутрь углеродного каркаса уже готовых молекул фуллерена может быть осуществлен длительным нагреванием при 600-1000 °С в присутствии газа при повышенном давлении (10-1000 МПа). Данный метод использовали для синтеза и исследования эндоэдральных молекул, содержащих атомы инертных газов Не, Ne, Ar, Кг, Хе и молекул СО, CN [41, 58]. Следует отметить, что содержание эндоэдральных молекул в продуктах синтеза обычно не превышает десятой доли процента.

Метод ионной имплантации синтеза эндоэдральных фуллеренов основан на бомбардировке полых фуллеренов ионами того элемента, который должен быть заключен в углеродный каркас молекулы фуллерена. Данный метод использован при получении эндоэдральных соединений, содержащих внутри себя атомы элементов повышенной химической активности. Так, с использованием этого метода в [59, 60]

В частности, в работе [49] сообщалось, что фуллерены, содержащие лантан и иттрий, могут быть получены путем лазерного испарения графитовых стержней, содержащих окислы металлов. Лазерно-десорбционный масс-спектрометрический анализ пленок сублимированной сажи, полученной лазерным испарением прутков La₂O₃ + графит, показал, что в продуктах реакции имеются в основном La@C₆₀, La@C₇₀, La@C₇₄, La@C_g2. Экстракция в толуоле приводила к получению преимущественно La@C_gr Подобные результаты были получены и при изучении иттрий-фуллереновых комплексов, где также наблюдалось более высокое содержание Y₂@C₈₂ [50]. Джонсон с сотр. [51] получил более значительные количества La@C_g2 и, используя методику электронного парамагнитного резонанса, показал, что лантан имеет заряд 3⁺, a C_g2 — заряд 3". В [52} отмечается, что металлофуллерены скандия значительно лучше растворяются в пиридине и дисульфиде углерода, чем в толуоле.

Следуя [53], опишем более детально методику получения ок-сидсодержащих графитовых стержней для получения металло-фуллеренов лантана, иттрия и скандия. В стержнях графита диаметром в четверть дюйма (6,45 мм) просверливался канал диаметром 4,32 мм на глубину 50,8 мм, который заполнялся смесью оксидов La₂O₃, Y₂O₃, Sc₂O₃ и графитового цемента в соотношении 1:1. В результате графитовые прутки содержали примерно 20 % по весу металлооксидов. Для затвердевания графитового цемента прутки нагревались и выдерживались при 140 °С в течение 4 часов. Затем прутки с целью дегазации нагревались до 1000 °С в вакууме. Приготовленные таким образом прутки, содержащие окислы металлов, распылялись обычным способом в электрической дуге.

Для анализа полученной сажи, экстрактов сажи и других продуктов реакции использовался десорбционный химический ионизационный масс-спектрометр с отрицательными ионами. С этой целью одна миллионная литра (или меньше) экстракта или суспензии сажи в толуоле наносилась на верхний конец пробной проволочки, которая помещалась внутрь источника, содержащего метан в качестве реактивного газа.

3.2Силы, действующие в движущейся жидкости

Силы, действующие на выделенную частицу движущейся жидкости, принято подразделять:

· на объёмные (массовые) силы, действие которых распространено по всему объёму частицы;

· на поверхностные силы, действие которых распространено по поверхности выделенной частицы жидкости.

Примеры:

а) Объёмная сила тяжести

Интенсивность объемной силы тяжести в бесконечно малой окрестности выбранной точке наблюдения характеризуют либо объемной плотностью сил тяжести

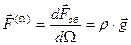, (2.1.11)

либо массовой плотностью сил тяжести

. (2.1.12)

б) Поверхностные силы нормального давления

Интенсивность нормальной составляющей силового воздействия на выделенный участок поверхности частицы среды характеризуют величиной давления, определяя его локальное значение формулой

, [P] = H/м² = Па. (2.1.13)

Давление сжатия в гидродинамике принято считать величиной положительной.

в) Поверхностные силы вязкого трения

Полное описание всех поверхностных сил даёт тензор напряжений, представляющий собой симметричный тензор второго ранга.

Рис. 2.1.7.К определению касательных напряжений в области гидродинамического пограничного слоя

Мы же ограничимся упрощённым рассмотрением одной из касательных составляющих тензора напряжения. Рассмотрим область гидродинамического пограничного слоя с ламинарным течением жидкости (рис 2.1.7). Пусть верхняя часть поверхности ∆S_у, ограничивающая выделенный объём ∆Ω, перпендикулярна оси OY. Значение касательного напряжения на рассматриваемой поверхности определяется равенством

, [τ_ху]=Н/м²=Па, (2.1.14)

где - проекция на ось ОХ составляющей касательной силы , действующей параллельно оси ОХ на контрольную площадку величиной ∆S_у, перпендикулярную оси ОУ. Путем обобщения экспериментов установлено, что в рассматриваемом случае значение касательного напряжения τ_ху подчиняется равенству

, (2.1.15)

где μ – так называемый динамический коэффициент вязкости [μ]=Н/(м² с^-1)=Па с. С ростом температуры динамический коэффициент вязкости μ для плотных жидкостей убывает, а для газовых сред возрастает. Оказалось целесообразным наряду с динамическим коэффициентом вязкости ввести в рассмотрение и т.н. кинематический коэффициент вязкости, определяемый соотношением

[υ]=м²/с. (2.1.16)

2.1.5.Уравнение Навье-Стокса

Рассмотрим нестрогий вывод уравнения движения несжимаемой вязкой жидкости (ρ=const, μ≠0). Для простоты компоненту тензора напряжений τ_ху будем обозначать далее через τ. Пусть ламинарный поток несжимаемой вязкой жидкости стекает вдоль вертикальной стенки, имеющей неограниченную протяжённость вдоль оси OZ (рис 2.1.8). Запишем проекцию на ось OX уравнения второго закона Ньютона для выделенной бесконечно малой частицы жидкости с объемом

dΩ = dxdydz

(1)

Рис. 2.1.8. К выводу уравнения движения несжимаемой вязкой жидкости

Проекции на ось ОХ имеют следующие составляющие сил, действующих на выделенную частицу жидкости:

· объемные силы тяжести

; (2)

· поверхностные силы давления

; (3)

· поверхностные силы вязкого трения

. (4)

Учтем, что и, следовательно,

. (5)

Подставив (2) – (5) в (1), получим

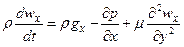. (6)

Уравнение (6) и аналогичные ему для осей OY и OZ, получаемые при строгом выводе, в полном формате будут иметь вид:

(2.1.17)

Совокупность уравнений (ρw₁S₁=ρw₂S₂) есть уравнение Навье-Стокса – уравнение движения несжимаемой вязкой жидкости, записанное в проекциях на оси прямоугольной декартовой системы координат. Переписанное в векторной форме, уравнение Навье-Стокса имеет вид

. (2.1.18)

Поделив обе части равенства (2.1.18) на плотность жидкости ρ и учитывая определения (2.1.16) для коэффициента кинематической вязкости, получим еще одну форму записи уравнения Навье-Стокса

. (2.1.19)

Подчеркнём ещё раз, что в правой части уравнения Навье-Стокса отдельными слагаемыми учитывается вклад объёмных сил тяжести, вклад нормальных составляющих поверхностных сил давления и вклад касательных сил вязкого трения.

Если в рамках решаемой задачи можно пренебречь вязкостью среды, то мы переходим к модели идеальной жидкости. Уравнение движения несжимаемой идеальной жидкости легко получить из уравнения Навье-Стокса, положив в (2.1.19) ν = 0

. (2.1.20)

Это уравнение принято называть уравнением Эйлера.

Билет 4

Билет 4.1 Углеродные нанотрубки. Методы получения УНТ. Структура УНТ. Хиральность нанотрубок.