Производство из углеродных нанотрубок электронных полевых эмиттеров

Углеродные нанотрубки могут быть использованы как электронные источники в двух различных видах: одиночные и многоигольчатые электронно-лучевые устройства.

1. Одно из возможных приложений – это одиночный электронно-лучевой инструмент как в электронном микроскопе, где может использоваться одиночная нанотрубка, как источник полевой эмиссии электронов, производящий высоко-когерентные электроны.

2. Наоборот, плоский панельный дисплей является популярным примером многолучевого инструмента, где сплошные или напыленные пленки нанотрубок приводят к большому числу независимых электронных лучей. Ниже рассмотрим различные методы, которыми можно реализовывать нанотрубные полевые эмиттеры и обсудим различные способы получения пленок из нанотрубок.(Одиночные нанотрубные эмиттеры (катоды), Нанотрубные пленки для полевых эмиттеров, Одиночный нанотрубный полевой эмиттер, Пленочные нанотрубные полевые эмиттеры)

6.6. Механизм полевой эмиссии

Почему нанотрубки являются хорошими эмиттерами? Высокие напряженности поля обеспечивает геометрическая форма нанотрубок. На самом деле условия эмиссии возникают в тонких металлических проволочках (заостренных) при значениях 2 - 3 В/мкм. Но, с другой стороны, нанотрубки не ведут себя при эмиссии как металлические проволочки. Следовательно, на такое поведение оказывает влияние структурное состояние углеродных нанотрубок. Картина эмиссии усложняется физическими и химическими факторами, которые возникают при производстве и очистке нанотрубок.

Предполагается, что графеновые слои на открытых концах формируют новые связи между атомами углерода, которые соответствуют sp³-конфигурации, вместо sp²-связей, свойственных графиту. Эти изменения в координации должны уменьшить высоту потенциального барьера и, следовательно, уменьшить работу выхода электронов.

Однако некоторые авторы пришли к выводу, что эмиссия электронов обусловлена энергетическими уровнями локализованных состояний на вершине нанотрубки. Действительно, теоретические подсчеты предсказывают наличие локализованных состояний на вершине трубки с плотностью электронных состояний, которая значительно отличается от плотности электронных состояний в основе трубки. Экспериментально это явление было подтверждено на МСУНТ и ОСУНТ с помощью СТМ. Имеются две точки зрения по поводу вышеприведенных гипотез. Если в эмиссии участвуют электроны нескольких энергетических уровней, то эмитируют те, которые занимают несколько ближайших к уровню энергии Ферми. Поскольку положение этих уровней сильно зависит от локальной атомной конфигурации (диаметр трубки, хиральности, наличию пентагонов и других дефектов), то наблюдается значительное различие эмитирующих токов от одной трубки к другой. Вторая точка зрения связана с тем, что эти электронные состояния на уровне Ферми имеют более высокую плотность по сравнению с объемом трубки. Поскольку эмиссионный ток непосредственно зависит от плотности состояний на уровне Ферми, то приходим к заключению, что эмитирующий ток для нанотрубок будет выше, чем у графита.

6.2Уравнение баланса энтальпии

Теоретические исследования и практика инженерных расчётов показали, что попытка записать уравнение энергетического баланса, учитывающего все виды энергии, во-первых, неосуществима с теоретической точки зрения, во-вторых, бесполезна с точки зрения практики. В этом пункте нам предстоит получить уравнение баланса энтальпии, лежащее в основе теоретического описания процессов переноса энергии в форме тепла.

Согласно первому закону термодинамики количество теплоты, переданное простой термомеханической системе, идет на увеличение её внутренней энергии и на работу против сил внешнего давления

(1)

При решении многих задач теплопереноса можно считать давление в системе постоянным (Р=const). В таких случаях согласно (1) имеем

(2)

где H =U+PV есть энтальпия системы. Т.е. количество тепла, поглощённое системой в изобарном процессе, равно изменению энтальпии системы. Вот почему нас интересует уравнение баланса энтальпии. Пусть:

• h- энтальпия единицы массы жидкости. [h]=Дж/кг;
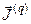• - вектор плотности потока энергии в форме тепла. Согласно определению есть количество энергии в форме тепла, пересекающее ежесекундно единичную контрольную площадку с нормалью , помещенную в окрестность выбранной точки наблюдения и неподвижную относительно лабораторной системы отсчёта. .
• - объемная плотность мощности тепловыделения в окрестности выбранной точки наблюдения в произвольный момент времени. Функция описывает в континуальном приближении либо действие источников джоулева тепла, либо теплообразование за счет гомогенных экзотермических химических реакций, например, реакций горения.

Рассмотрим баланс энтальпии в контрольном объеме , неподвижном относительно лабораторной системы отсчета и помещённом в окрестности выбранной точки наблюдения с координатами (x, y, z). Дальнейшие рассуждения будут практически повторять рассуждения пункта (2.2.1). Пусть

(1)

есть изменение энтальпии в контрольном объеме dΩ за время dt. Это изменение обусловлено:

а) разностью между количеством энергии в форме тепла, втекающим в контрольный объём dΩ и вытекающим из него вдоль координатной оси ОХ за время dt (рис 2.3.1)

. (2)

Рис.2.3.1 К выводу уравнения баланса энтальпии

Разлагая величину в ряд по малому параметру dx, и ограничиваясь линейным приближением, представим формулу (2) в виде

; (3)

б) разностью между количеством энергии в форме тепла, втекающим в контрольный объём dΩ и вытекающим из него вдоль координатных осей ОY и OZ за время dt. Равенства, учитывающие влияние переноса тепловой энергии вдоль указанных осей, будут иметь вид, аналогичный (3)

, (4)

; (5)

в) производством энтальпии в контрольном объеме dΩ за счет действия источников тепла распределенных по объему жидкости с плотностью

(6)

Так как в контрольном объёме dΩ

, (7)

то, учитывая (1)-(6), получаем уравнение баланса энтальпии в виде

(2.3.1)

2. Плотность теплового потока. Закон Фурье

Перенос энергии в форме тепла в движущейся жидкости реализуется главным образом двумя механизмами: теплопроводностью и конвекцией (лучистый теплообмен во внимание принимать не будем, пологая, что температура среды не слишком велика). Поэтому для полной плотности потока энергии в форме тепла можем записать

(2.3.2)

Теплопроводность - это процесс распространения тепла от более нагретых элементов среды к менее нагретым, не связанный с макроскопическим перемещением вещества, а обусловленный энергообменом между атомами и молекулами, совершающими хаотическое тепловое движение. Для изотропных тел плотность потока тепла, передаваемого по механизму теплопроводности , подчиняется закону Фурье:

. (2.3.3)

Здесь λ- индивидуальная материальная характеристика среды, называемая коэффициентом теплопроводности. . Если в рассматриваемом потоке жидкости перепад температур не слишком велик, то для упрощения дальнейших рассуждений можно принять λ=const.

Конвективный теплоперенос – это перенос тепловой энергии вместе с потоком движущейся жидкости. Плотность потока тепловой энергии, передаваемой путем конвекции, определяется выражением:

. (2.3.4)

В справедливости этого равенства можно убедиться путем таких же рассуждений, что и в п.2.2.3.2 при получении формулы .

Совместный перенос теплоты теплопроводностью и конвекцией называют конвективным теплообменом (теплопереносом). Суммируя выражение (2.3.3) и (2.3.4) для полной плотности потока энергии в форме тепла получаем

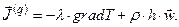(2.3.5)

3. Уравнение энергии

Уравнением энергии принято называть дифференциальное уравнение, которому подчиняется поле температур движущейся жидкости. Для вывода уравнения энергии воспользуемся уравнением баланса энтальпии (2.3.1)

(1)

и выражением (2.3.5) для полной плотности потока энергии в форме тепла:

. (2)

Будем рассматривать удельную энтальпию как функцию температуры и давления. Тогда

(3)

Примем для простоты, что жидкость несжимаема и потому

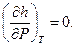(4)

В этом случае

(5)

где с_P – удельная теплоемкость жидкости при постоянном давлении. [с_P] = Дж/(кг·К). Примем, что в рассматриваемом диапазоне температур теплоемкость жидкости можно считать величиной постоянной

. (6)

С учетом (5) и (6) левая часть (1) может быть представлена в виде

(7)

Подставляя (2) в (1) и учитывая (7), для несжимаемой жидкости (ρ = const), с постоянным коэффициентом теплопроводности (λ = const) и постоянной удельной изобарной теплоёмкостью (с_Р = const) получим

(8)

Рассмотрим второе слагаемое правой части (8). Согласно известной формуле векторного анализа для несжимаемой жидкости находим

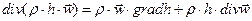. (9)

Для несжимаемой жидкости согласно уравнению неразрывности

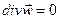, (10)

вследствие чего формула (9) упрощается и принимает вид

. (11)

Интегрируя (6) в соответственных пределах от некоторой стандартной температуры Т₀ до текущего её значения T, получаем

. (12)

С учетом (12) согласно (11) для рассматриваемой жидкости находим

. (13)

С помощью (13) уравнение (8) можно преобразовать к виду

. (2.3.6)

Учитывая определение материальной производной, после деления на ρ∙с_P≠0 получаем

. (2.3.7)

Величину

(2.3.8)

принято называть коэффициентом температуропроводности. [a]=м²/с. Уравнение (2.3.7) есть уравнение конвективного теплообмена или уравнение энергии. Оно, как и уравнение диффузии, относится к классу параболических уравнений в частных производных второго порядка. Математические методы решения этих уравнений одни и те же. Так же как и уравнение конвективной диффузии, уравнение энергии (2.3.7) следует рассматривать совместно с уравнением движения жидкости (для определения поля скоростей), либо поле скоростей жидкости должно быть задано.

3 Уравнение нестационарной теплопроводности в неподвижной среде

Для неподвижной среды 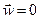и уравнение энергии (2.3.7) принимает вид

. (2.3.9)

Это и есть уравнение нестационарной теплопроводности. Оно применимо в тех случаях, когда преобладает только один механизм теплопереноса, а именно, процесс теплопроводности.

2.4. Система уравнений переноса

Нетрудно привести примеры технологических процессов, в которых имеются неизотермические потоки неоднородной по составу жидкой смеси. В таких условиях процессы переноса тепла и вещества подчиняются системе взаимосвязанных дифференциальных уравнений в частных производных для полей давления, скорости жидкости, концентраций примесных компонентов и температуры. Эту систему принято называть системой уравнения переноса. В общем случае она очень сложна, и для получения решения в численном виде необходимо принимать ряд упрощающих предположений.

Во многих практически важных случаях можно принять следующие упрощения:

• плотность жидкости может изменяться только благодаря изменению её температуры согласно закону:

, (2.4.1)

где коэффициент термического расширения можно считать величиной постоянной в рабочем диапазоне температур, ;

• диффузионные потоки примесных компонентов подчиняются первому закону Фика:

(i = 2,3,....к) (2.4.2)

В самом деле, при малых концентрациях, как показывает эксперимент, взаимным влиянием примесей на диффузию можно пренебречь, а коэффициенты диффузии считать величинами, зависящими только от температуры. Если к тому же перепад температур в системе не слишком велик, то можно считать все коэффициенты диффузии постоянными величинами (D_i = const);

• плотность потока теплопроводности подчиняется закону Фурье:

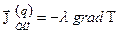, (2.4.3)

где коэффициент теплопроводности l можно считать величиной постоянной, если перепад температур в системе не слишком велик;

• гомогенные химические реакции в системе отсутствуют:

, (i = 1,2,....к). (2.4.4)

Отметим, что это предположение не мешает учитывать, по крайней мере в термодинамическом приближении, гетерогенные химические реакции, протекающие на поверхности раздела фаз, и являющиеся основой для получения очень многих материалов электронной техники методом химического осаждения из газовой фазы.

В тех случаях, когда указанные предположения можно считать соответствующими действительности, поля проекций скоростей жидкости w_x = w_x( ,t), w_y = w_y( ,t) и w_z = w_z ( , t), концентраций примесных компонентов N_i = N_i ( , t), температуры T = T ( , t) и давления Р = Р ( , t) могут быть, в принципе, найдены путем решения системы уравнений переноса, включающей:

1. Уравнение неразрывности

. (2.4.5)

2. Уравнения конвективной диффузии

, (i = 2,3,4....к). (2.4.6)

3. Уравнение Навье– Стокса в форме

. (2.4.7)

В левой части этого уравнения плотность жидкости считается постоянной. В правой же части учитывается зависимость (2.4.1) плотности смеси от температуры, что позволяет включить в число учитываемых факторов объёмные силы естественной конвекции.

4. Уравнение энергии

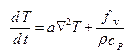. (2.4.8)

Для полной постановки задачи помимо уравнений (2.4.5) – (2.4.8) необходимо задать так называемые условия однозначности, дающие математическое описание всех частных особенностей рассматриваемого процесса. Условия однозначности включают:

• геометрические условия: размеры и формы тел системы, условия симметрии;
• физические характеристики среды и различные кинетические коэффициенты , b, m и т.д.;
• явное описание объемных источников теплоты;
• начальные условия для всех искомых функций;
• граничные условия для всех искомых функций.

Система уравнения переноса - это в общем случае система нелинейных дифференциальных уравнений в частных производных. Общие методы аналитического решения таких систем отсутствуют. В сравнительно простых частных случаях практический интерес может представлять решение отдельных уравнений системы. Но даже и в этих простых случаях получить аналитическое решение удается далеко не всегда, и необходимо делать дополнительные упрощающие предположения

Билет №6

3.Дипольные моменты и структура кристаллов.Принцип Неймана.Полярные классы кристалов.Сегнетоэлектрики.

1. Дипольные моменты и структура кристаллов Структуру кристаллического диэлектрика можно в первом приближении рассматривать как систему электрических зарядов, определенным образом расположенных в пространстве в соответствии с законами симметрии. Химические связи между структурными элементами в предельных случаях могут быть ионными или ковалентными. В структурах большинства реальных кристаллов химические связи между атомами являются промежуточными: они включают в себя как электростатическое взаимодействие структурных элементов, обусловленное смещением электронных оболочек, так и квантовое взаимодействие, вызванное их перекрытием.

Электростатическое взаимодействие структурных элементов можно учесть, приписав каждому атому некоторый эффективный заряд е^*.

e* = Ke^ион . (1.1)

Для идеальных ионных кристаллов эффективные заряды, естественно, равны валентностям соответствующих ионов, т.е. К=1. Для кристаллов с ковалентными связями эффективные заряды должны равняться нулю (К=0).

Электрические свойства кристаллов определяются как величиной и знаком эффективных зарядов структурных элементов, так и их взаимным расположением, причем количественной характеристикой распределения электрических зарядов в структуре кристалла является электрический момент.

Для системы точечных зарядов электрический момент равен:

(1.2)

где - радиус-вектор, проведенный из произвольно выбранной точки кристалла к i-му заряду. При непрерывном распределении заряда с объемной плотностью r(r) электрический момент можно записать

(1.3)

Электрический момент пары зарядов одинаковой величины, но разных по знаку называется дипольным моментом

(1.4)

где - радиус-вектор, проведенный от отрицательного заряда к положительному заряду.

Если в системе имеется некоторое распределение зарядов, то ее эквивалентный дипольный момент может быть рассчитан как произведение суммарного заряда одного знака на расстояние R между электрическими центрами тяжести положительных и отрицательных зарядов:

(1.5)

где (1.6)

В системе СИ за единицу измерения дипольного момента d принимается [Кл×м].

Если в элементарной ячейке кристалла "центры тяжести" всех положительных и отрицательных зарядов структурных элементов совпадают, то все дипольные моменты структуры равны нулю. Такие кристаллы будем называть бездипольными. В отличие от них дипольными кристаллами называются кристаллы, в которых имеется асимметрия в распределении электрических зарядов за счет несовпадения "центров тяжести" положительных и отрицательных зарядов. Существование дипольных моментов можно условно рассматривать как следствие поляризации структурных элементов под действием внутреннего электрического поля, создаваемого всеми зарядами и диполями структуры.

При макроскопическом описании поляризации, а также электропроводности, пьезоэлектрического эффекта, упругих свойств и др. можно не учитывать дискретность структуры и рассматривать кристалл как непрерывную однородную, но анизотропную среду. В этом случае симметрия кристаллов как непрерывной анизотропной среды описывается 32 точечными группами симметрии, а не 230 пространственными группами, если рассматривать кристалл как дискретную анизотропную среду. Поскольку симметрия физических свойств кристалла, определяется его точечной группой, все кристаллы делят на 32 кристаллографических класса кристаллов, соответствующие 32 точечным группам симметрии.

Используя известный из кристаллофизики принцип Неймана, можно произвести отбор классов кристаллов, которые должны обладать теми или иными физическими свойствами.

2 Принцип Нейманаформулируется следующим образом: элементы симметрии точечной группы кристалла содержатся среди элементов симметрии свойства. Другими словами, симметрия кристалла не может быть выше, чем симметрия любого его физического свойства. Это означает, что симметрия кристалла должна быть подгруппой точечной группы, описывающей физическое свойство, либо иметь группу симметрии этого свойства.

Зная симметрию полярного вектора ¥ mm, можно показать, что кристаллы, имеющие отличный от нуля атомный дипольный момент, то есть полярные кристаллы, должны по своей точечной симметрии принадлежать к 10 полярным классам, являющимися подгруппами группы симметрии полярного вектора. Такими подгруппами группы ¥ mm являются полярные точечные группы симметрии: 1, 2, 3, 4, 6, m, mm2, 3m, 4mm, 6mm. Кристаллы, принадлежащие к этим классам, называются пироэлектрическими. Примером пироэлектриков являются кристаллы турмалина, сахара, сульфата лития и др.

По наличию или отсутствию полярных направлений в кристаллах все 32 кристаллографических класса можно разделить на 3 части. К первой относятся уже рассмотренные выше полярные кристаллы. Ко второй части кристаллических классов принадлежат кристаллы, в которых нет полярных направлений. У таких кристаллов расположение положительных и отрицательных зарядов является центросимметричным, и центры тяжести зарядов каждого знака совпадают друг с другом. Такие кристаллы называются неполярными. Симметрийный признак неполярных кристаллов - наличие центра симметрии. Этому требованию удовлетворяют 11 классов: m3m, m3, 6/mmm, 4/mmm, mmm, m, 6/m, 4/m, 2/m, , . Оставшиеся 11 кристаллических классов: 3m, 432, 23, m2, 622, , 3/2, 2m, 422, , 222 имеют симметрию так называемых полярно-нейтральных кристаллов. В таких кристаллах есть полярные направления, но нет особенных полярных направлений, а существующие равные полярные направления образуют совокупность полярных векторов, в сумме равную нулю.

Итак, из 32 кристаллографических классов 11 характеризуются наличием центра симметрии. Центросимметричный кристалл естественно не может обладать полярными свойствами. Если к такому кристаллу приложить однородное механическое напряжение, то произойдет небольшое смещение зарядов в решетке, однако, из-за наличия центра симметрии эти относительные смещения окажутся скомпенсированными. Если к центросимметричному кристаллу приложить электрическое поле, то он деформируется, однако эта деформация будет оставаться неизменной при перемене знака приложенного поля. Другими словами деформация пропорциональна квадрату приложенного поля. Этот эффект называется электрострикцией. Он существует во всех средах: кристаллических и аморфных, твердых и жидких.

Остающийся 21 кристаллографический класс не имеет центра симметрии. Кристаллы этих классов могут иметь одну или несколько полярных осей и, следовательно, могут обладать векторными и тензорными свойствами. Кристаллы всех ацентричных классов (кроме кубического класса 432) обнаруживают пьезоэлектрический эффект. Пьезоэффект - это свойство кристалла приобретать электрическую поляризацию (поляризоваться) при приложении механических напряжений или деформироваться под действием приложенного электрического поля. Пьезоэффект в отличие от электрострикции является линейным по полю эффектом.

Из 20 пьезоэлектрических классов 10 характеризуются тем, что имеют особенные полярные оси. Кристаллы этих классов спонтанно поляризованы. Спонтанную поляризацию, как правило, нельзя обнаружить по наличию зарядов на поверхности кристалла, поскольку эти заряды скомпенсированы проводимостью или за счет двойникования. Однако если изменять температуру кристалла, то изменяется поляризация и на гранях, перпендикулярных полярной оси, возникают электрические заряды. Такой эффект называется пироэлектрическим. Поэтому 10 классов, имеющих особенную полярную ось, называются пироэлектрическими.

Сегнетоэлектрические кристаллы принадлежат к семейству пироэлектриков. Однако они составляют только часть этого семейства и характеризуются тем, что в сегнетоэлектриках направление спонтанной поляризации может быть изменено на противоположное или повернуто на некоторый угол (реориентировано) внешним электрическим полем. Следовательно, необходимым условием того, чтобы кристалл был сегнетоэлектриком, является принадлежность его к одному из 10 полярных классов. Но это условие не является достаточным, поскольку поляризация должна быть обратимой. Таким образом, сегнетоэлектрик - это пироэлектрик с обратимой или реориентируемой поляризацией.

Билет 7

Билет 7.1 Особенности электрических свойств аморфных металлических сплавов, сопоставление с кристаллическими аналогами.