Понятие оптимизационных задач и оптимизационных моделей

Экономико-математические задачи, цель которых состоит в нахождении наилучшего (оптимального) с точки зрения некоторого критерия или критериев варианта использования имеющихся ресурсов (труда, капитала и пр.), называются оптимизационными.

Оптимизационные задачи (03) решаются с помощью оптимизационных моделей (ОМ) методами математического программирования.

Структура оптимизационной модели состоит из целевой функции, области допустимых решений и системы ограничений, определяющих эту область. Целевая функция в самом общем виде, в свою очередь, также состоит из трех элементов:

• управляемых переменных;

• неуправляемых переменных;

• формы функции (вида зависимости между ними).

Область допустимых решений - это область, в пределах которой осуществляется выбор решений. В экономических задачах она ограничена наличными ресурсами, условиями, которые записываются в виде системы ограничений, состоящей из уравнений и неравенств.

Если -система ограничений несовместима, то область допустимых решений является пустой. Ограничения подразделяются: а) на линейные (/ и // ) и нелинейные (/// и IV) (рис. 5.1);

б) детерминированные (А, В) и стохастические (группы кривых С,) (рис. 5.2).

Стохастические ограничения являются возможными, вероятностными, случайными.

ОЗ решаются методами математического программирования, которые подразделяются:

• на линейное программирование;

• нелинейное программирование;

• динамическое программирование;

• целочисленное программирование;

• выпуклое программирование;

• исследование операций;

• геометрическое программирование и др.

Главная задача математического программирования - это нахождение экстремума функций при ограничениях в форме уравнений и неравенств.

Рассмотрим 03, решаемые методами линейного программирования.

§2. Оптимизационные задачи с линейной зависимостью между переменными

Пусть:

bj - количество ресурса вида i (i = 1, 2, т); aij - норма расхода /-того ресурса на единицу у'-того вида продукции;

Xj - количество продукции вида у (j' - 1,2, n);

Cj - прибыль (доход) от единицы этой продукции (в задачах на минимум - себестоимость продукции).

Тогда ОЗ линейного программирования (ЛП) в общем виде может быть сформулирована и записана следующим образом:

Найти переменные х,- (j = 1,2,..., п), при которых целевая функция

F(x) =

была бы максимальной (минимальной), не нарушая следующих ограничений:

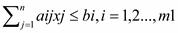
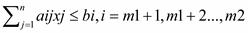
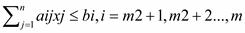
Все три случая можно привести к так называемой канонической форме, введя дополнительные переменные:

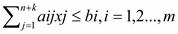
Где к - количество дополнительных переменных, и условие неотрицательности искомых переменных: х_;> 0.

В результате решения задачи находится некий план (программа) работы некоторого предприятия. Отсюда и появилось слово «программирование». Слово «линейное» указывает на линейный характер зависимости как в целевой функции, так и в системе ограничений. Следует еще раз подчеркнуть, что задача обязательно носит экстремальный характер, т.е. состоит в отыскании максимума или минимума (экстремума) целевой функции.

§7. Двойственная задача ЛП

Двойственная задача ЛП может быть сформулирована следующим образом:

найти переменные у,- (г = 1, 2,т), при которых целевая функция была бы минимальной

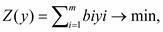
не нарушая ограничении

Yi>=0 (i=1,2,…, m).

Данная задача называется двойственной (симметричной) по отношению к прямой задаче, сформулированной во втором параграфе главы. Однако правильным будет и обратное утверждение, так как обе задачи ЛП связаны между собой теоремами двойственности.

Первая теорема двойственности.Если обе задачи имеют допустимые решения, то они имеют и оптимальное решение, причем значение целевых функций у них будет одинаково

F(x)=Z(x) или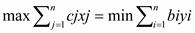

Если же хотя бы одна из задач не имеет допустимого решении, но ни одна из них не имеет оптимального решения.

Вторая теорема двойственности (теорема о дополняющей нежесткости). /Для того чтобы векторы X = (x1, x2, …., xn) и

Y=(y1, y2, …, yn) были оптимальными решениями соответственно прямой и двойственной задачи, необходимо и достаточно чтобы выполнялись следующие условия:

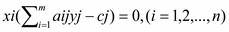
Следствие 1. Пусть оптимальное значение некоторой переменной двойственной задачи строго положительно.

Yi>0

Тогда из условия 1 получим

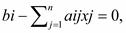или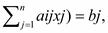

Экономический смысл данных выражений можно интерпретировать в следующей редакции. Если объективно обусловленная оценка некоторого ресурса больше нуля (строго положительна), то этот ресурс полностью (без остатка) расходуется в процессе выполнения оптимального плана.

Следствие2. Пусть для оптимального значения некоторой переменной х, прямой задачи выполняется условие строгого неравенства

Тогда, основываясь на том же первом условии (1), можно заключить, что уi- = 0.

Экономически это означает, что если в оптимальном плане какой-то ресурс используется не полностью, то его объективно обусловленная оценка обязательно равна нулю.

§8. Решение двойственной задачи ЛП

Ранее (§6) мы рассматривали прямую задачу ЛП:

F(x) = 180Х1, + 20х₂ -> max

0.5Х1, + 0,04х₂ < 200

12x1 + 0,6х₂ < 1800

Х1, >= 80

Х1х2>= 0.

В системе неравенств должны быть однотипные знаки «меньше или равно». Поэтому неравенство Х\ > 80 умножим на -1 и поменяем знак неравенства на противоположный.

Z(y) = 200y1 + 1800у₂ - 80у₃ -> min

0,5у1, + 12у₂ – у3 >= 180

0,04у1, + 0,6у₂ >= 20

У1, У2 >= 0.

Ограничение на целочисленность переменных здесь не требуется.

Решение прямой задачи дало следующие результаты: X1 = 80; х₂ = 1400; F(x) = 42400.

В результате решения двойственной задачи получим у1, =0; у₂ = 33,3; у₃ = 220; Z(y) = 42400.

Объективно обусловленная оценка у₁ = 0 указывает на то, что у нас избыток древесины: y₂ = 33,3, т.е. больше нуля. Значит этот ресурс (труд) полностью используется в оптимальном плане. значение целевой функции Z(y) равно F(x) = 42400. Это свидетельствует о том, что найденное решение оптимально.

Геометрическая интерпретация ОЗ линейного программирования

До приобретения мебельного цеха Василий Тимофеев имел небольшую столярную мастерскую, где он мог трудился вместе со своим сыном по 9 часов в день, изготавливая тару двух видов – А и В, расходуя для этого ежедневно 4 куб. м древесины и 18 кг металла. Необходимо найти ежедневный оптимальный план производства двух видов тары(x1 и x2), при котором прибыль Василия была бы максимальной, а имеющиеся ресурсы использовались бы наилучшим образом

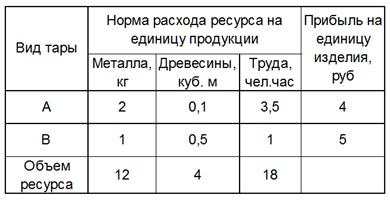
Оптимизационная модель задачи запишется следующим образом:

а) целевая функция:

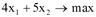
б) ограничения:

2 x1 + х2 12 (ограничение по металлу);

0,1x1 + 0,5х2 4 (ограничение по древесине);

3,5x1 + х2 18 (ограничение по труду).

в) условие неотрицательности переменных:

Х1=2,2

Х2= 7,5

Прибыль = 46,3 руб.

Понятие балансового метода и балансовых моделей. Принципиальная схема межотраслевого баланса. Экономико-математическая модель МОБ. Определение конечной и валовой продукции отраслей.

Балансовый метод – это метод взаимного сопоставления имеющихся материальных, трудовых и финансовых ресурсов и потребностей в них.

Балансовая модель – это система уравнений, которые удовлетворяют требованиям наличия ресурсов и потребностей в них.

Есть несколько видов балансовых моделей:

• трудовые, материальные, финансовые

• межотраслевые

• межотраслевые балансы с учетом экономических факторов

• матричные техпромфинпланы

• межрегиональные макроэкономические модели (пример - модель "Затраты-выпуск", полученная в 1930 г. американским экономистом В. Леонтьевым).