
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Модель Шарпа. САРМ.
Ожидаемую доходность актива можно определить с помощью так называемых индексных моделей. Их суть состоит в том, что изменение доходности и цены актива зависит от ряда показателей, характеризующих состояние рынка, или индексов. В модели Шарпа представлена зависимость между ожидаемой доходностью актива и ожидаемой доходностью рынка. Она предполагается линейной. Уравнение модели имеет следующий вид:
 либо
либо
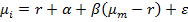 , где
, где
µi – доходность i-ого актива
µm – рыночная доходность
α – оценка рынком перспектив компании – надбавка за хорошее управление компанией
r – безрисковая ставка
β – коэффициент чувствительности актива к ситуации на рынке (  )
)
ε – независимая случайная ошибка (индивидуальный риск актива)
Приведенное уравнение является уравнением регрессии. Если его применить к широко диверсифицированному портфелю, то значения случайных переменных (ei) в силу того, что они изменяются как в положительном, так и отрицательном направлении, гасят друг друга, и величина случайной переменной для портфеля в целом стремится к нулю. Поэтому для широко диверсифицированного портфеля специфическим риском можно пренебречь.

CAPM (Capital assets pricing model) – модель оценки индивидуального актива. Модель связывает ожидаемую доходность и систематический риск (бета актива) и демонстрирует, как рынок должен оценить индивидуальный актив в зависимости от его рискового класса. CAPM предполагает, что существует только один вид риска отдельного актива, от которого зависит его доходность – это чувствительность к рыночному риску. Таким образом, все многообразие рисков, которым подвергается любой конкретный актив, сведено только к одному риску - рыночному.
Графиком CAPM является SML (security market line). SML является графиком отдельного актива.

Теперь мы видим, от чего зависит доходность ценной бумаги. Она зависит от:
r – безрисковой доходности;
μm – доходности рыночного портфеля;
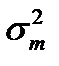 – вариации рыночного портфеля;
– вариации рыночного портфеля;
 – ковариации доходности i-го актива с доходностью рынка в целом.
– ковариации доходности i-го актива с доходностью рынка в целом.
Причем, первые три фактора являются одинаковыми абсолютно для всех активов. Единственное, чем активы различаются, – это величинами ковариации. Следовательно, различия в доходностях активов могут быть объяснены исключительно этим параметром и ничем больше.
Поскольку приведенное выше уравнение представляет собой уравнение прямой, то графически зависимость выражается так называемой линией рынка ценных бумаг, которую можно изобразить следующим образом.
| σmi |
| μ |
| SML |
| μm |
| M |
| r |

|
бета – это мера того, насколько поведение акции похоже на поведение рынка в целом.
Бета измеряет вклад актива в портфельный риск. Бета средней акции равна единице.
β > 1 – агрессивные акции. Сильно зависят от рыночной конъюнктуры.
β = 1 – средние акции. Средне зависят от рыночной конъюнктуры
β < 1 – консервативные акции. Слабо зависят от рыночной конъюнктуры
Беты обладают свойством аддитивности.
САРМ, по сути, является гипотезой, поскольку проверена быть не может. Она не поддается верификации по нескольким причинам, главными из которых будут следующие:
1. САРМ имеет дело с ожидаемыми величинами – как доходностями, так и волатильностями. Проверка же предполагает, что мы используем фактические данные, а не ожидаемые. Поскольку ожидаемые величины наблюдать нельзя, то и САРМ проверить нельзя.
2. САРМ предполагает, что рынок находится в равновесии. Однако это, во-первых, гипотеза, во-вторых, можно задать различные типы равновесия, причем все они будут эмпирически неопределимы.
3. Модель САРМ основывается на гипотезе о поведении инвестора и, в частности, о форме кривой безразличия. Поскольку в модели появляются полезности, то она непроверяема по той причине, что еще никто эти полезности не измерил.
Дата добавления: 2015-04-18; просмотров: 288; Мы поможем в написании вашей работы!; Нарушение авторских прав |