ALM. Чувствительность облигаций к изменению ставки процента. Дюрация и выпуклость.

ALM (asset-liability management) – это такая практика управления бизнесом, при которой решения и действия направлены на координацию активов и пассивов. ALM может рассматриваться как непрерывный процесс формулирования, внедрения, мониторинга и пересмотра стратегий, связанных с активами и пассивами, с целью достижения финансовых целей организации при заданных терпимости к риску и других ограничениях.

ALM применяется для минимизации балансовых рисков, т.е. рисков, связанных с рассогласованием активов и пассивов. Целевой функцией, достигаемой при данном подходе, обычно выбирается снижение чувствительности стоимости портфеля к изменению процентной ставки.

Активы с разным сроком погашения по разному реагируют на изменение ставки процента, т.е. обладают разной чувствительностью к ее изменению.

Так, например, при изменении ставки процента на 1% современная стоимость 5-ти летней облигации снизится на 4,2%, а 10-ти летней – на 7,4%.

Для оценки чувствительности актива к изменению ставки процента применяется показатель дюрация.

Поскольку функция цены облигация является функцией от доходности и является нелинейной функцией, то она может быть разложена в ряд Тейлора:

Или

, где

B – цена облигации;

r – доходность (для ценных бумаг обычно обозначаются у);

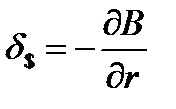- первая производная (долларовая дюрация);

- вторая производная (долларовая выпуклость).

Долларовая дюрация показывает, на сколько долларов изменится цена облигации при изменении ставки процента на 1%.

Разделим и левую и правую часть на B

, где

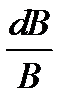- процентное изменение цены облигации;

- модифицированная дюрация;

- обыкновенная выпуклость.

Модифицированная дюрация показывает, на сколько процентов изменится цена облигации при изменении ее доходности на 1%. Следовательно, чем выше дюрация, тем выше чувствительность цены облигации к изменению ставок процента на рынке, поскольку реакция выше.

Умножив модифицированную дюрацию на (1+r), получим дюрацию Маколи: (в годах)

Дюрация Маколи – эффективный срок жизни актива, то ест период времени, в течение которого от данного актива будет получена основная сумма доходов.

Дюрация является мерой процентного риска. Чем выше дюрация, тем больше риск данного актива.

Выпуклость (convexity) – показатель несимметричности реакции цены на изменение доходности.

При равной дюрации, чем больше выпуклость, тем больше рост цены при падении доходности и, следовательно, тем меньше снижение цен при росте доходности. Следовательно, если две облигации имеют одинаковую дюрацию, более предпочтительной будет та, у которой выпуклость больше (лучше та, которая более выпукла).

Большая выпуклость показывает, что чем сильнее изменения ставки процента, тем меньше ее относительный эффект.