
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Процесс гибели-восстановления и его использование для расчета надежности восстанавливаемых систем.
Расчет над. восстан. систем с нагр. и ненагр. резервом.
Резервирование замещением с ненагруженным резервом. Система состоит из m одинаковых элементов, в каждый момент времени работает один элемент; если он откажет, то заменяется очередным резервным. Каждый отказавший элемент немедленно начинает восстанавливаться, причем число ремонтных бригад таково, что все отказавшие элементы восстанавливаются независимо друг от друга (такой вид восстановления называется неограниченным).
Восстановленные элементы переводятся в резерв. Отказ системы наступает, если откажут все m элементов. Заданы: l – интенсивность отказов элементов, m – интенсивность восстановления элемента. Для марковского процесса (экспоненциального закона распределения) l=1/t0, t0 – наработка на отказ элемента , m=1/tв, tв – среднее время восстановления. Состояние системы полностью описывается числом отказавших элементов:
0,1,2,...,m-1, m; состояние 0 – система полностью исправна, состояние m – система отказала. Нетрудно видеть, что работа системы представляет собой процесс гибели-восстановления. Подставив соответствующие значения интенсивностей отказов и восстановлений в формулы  (2.14),
(2.14), 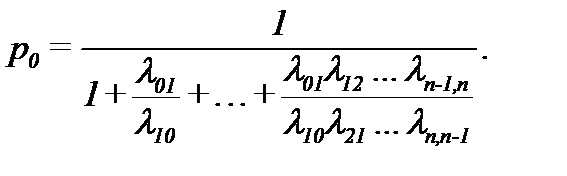 , (2.15)
, (2.15)
получим известные формулы Эрланга:
 (4.5)
(4.5)
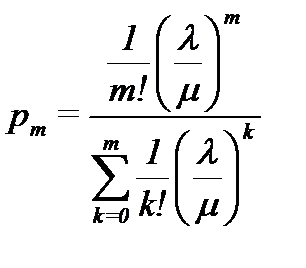 . (4.6)
. (4.6)
Вероятность pm численно равна коэффициенту простоя kп:
 . (4.7)
. (4.7)
Формулы (4.5), (4.6) заметно упрощаются, если ввести относительное время восстановления r=tв/t0=l/m.
 ,
,  .
.
Так как восстановление одновременно выполняют m бригад, интенсивности выхода из состояния отказа равна mm, среднее время восстановления системы Тв обратно пропорционально интенсивности выхода из состояния отказа Тв=1/mm и выражение для наработки на отказ получится в следующем виде:
 . (4.8)
. (4.8)
При обычном для высоконадёжных систем условии l<<m (r<<1) формулы (4.6), (4.8) существенно упрощаются
 ,
,  (4.9)
(4.9)
В случае ограниченного восстановления, если имеется всего одна ремонтная бригада Подставив значения интенсивностей отказов и восстановлений в формулы (2.14), (2.15), получим выражение для вероятности p0
 . (4.10)
. (4.10)
В выражении для вероятности p0 (4.9) стоит сумма геометрической прогрессии с первым членом 1 и знаменателем r=l/m, откуда окончательно получается
 , (4.11)
, (4.11)
 . (4.12)
. (4.12)
Коэффициенты готовности и простоя рассчитываются по формулам (4.7). С учётом того, что работает всего одна ремонтная бригада, интенсивности выхода из состояния отказа равна m, и наработка на отказ рассчитывается по формуле
 (4.13)
(4.13)
При условии l<<m (r<<1) формулы (4.12), (4.13) упрощаются
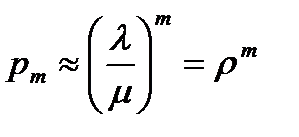 ,
, 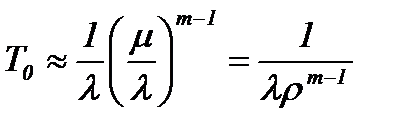 . (4.14)
. (4.14)
Расчет надеж. восст. систем с ненадеж. перекл.
Учет отказов переключателя. Для переключателей характерны два типа отказов:
- несрабатывание в моменты, когда он должен переключиться, показатель надёжности по этому типу отказов – вероятность срабатывания a;
- ложное срабатывание, т.е. несанкционированное переключение, которое может произойти в любой момент времени, показатель надёжности по этому типу отказов – интенсивность ложных срабатываний lл.
Рассмотрим систему, состоящую из двух элементов, основного (О), резервного (Р) и переключателя (П). Резервирование замещением, резерв облегчённый, интенсивность отказов работающего элемента l0, интенсивность отказов элемента, находящегося в резерве, lр, 0<lр<l0. Отказы резервного элемента явные. При отказе основного элемента переключатель с вероятностью a производит переключение на резервный, а с вероятностью (1-a) происходит отказ системы. Переключатель может срабатывать ложно с интенсивностью lл. После отказов элементы и переключатель начинают немедленно восстанавливаться, и после восстановления вновь включаются в работу. Восстановление неограниченное, интенсивность восстановления mв. При отказе системы восстановление переключателя производится одновременно с восстановлением элементов.
Чтобы проще было составить граф процесса отказов-восстановлений, состояния элементов системы следует закодировать. Элементы могут находиться в одном из двух состояний – работоспособное «0» и отказовое «1». Переключатель может находиться в одном из трёх состояний – работоспособное «0», отказ-несрабатывание «1» и отказ - ложное срабатывание «2». Система (С) может находиться в одном из двух состояний – работоспособное e0 и отказовое e1. Отказ системы наступает, если откажут оба элемента основной и резервный или в момент отказа основного элемента не сработает переключатель, или откажет резервный элемент и, несмотря на работоспособное состояние основного элемента, произойдёт переключение на резервный. Коды возможных состояний системы приведены в таблице 4.1.
Таблица 4.1.
| С | О | Р | П | Состояния |
| e0 | Система полностью исправна | |||
| e0 | Отказал основной элемент, произошло переключение не резерв. | |||
| e1 | Отказал основной элемент, не сработал переключатель (отказ типа несрабатывание). | |||
| e0 | Отказал резервный элемент. | |||
| e1 | Отказали основной и резервный элементы | |||
| e0 | Произошло ложное переключение с основного элемента на резервный. | |||
| e1 | Отказал резервный элемент, и произошло ложное переключение на него. |
Граф переходов марковского процесса содержит семь состояний. Состояния удобно располагать вверху вниз или слева направо по мере увеличения числа отказов, при этом желательно, чтобы чётко разделялись подмножество работоспособных состояний системы E0 и подмножество состояний отказа E1. Граф переходов марковского процесса представлен на
.
Переход «000» ® «100» происходит при отказе основного элемента и успешном срабатывании переключателя с интенсивностью l0a, переход «000» ® «101» происходит при отказе основного элемента и несрабатывании переключателя с интенсивностью l0(1-a). Переход «000» ® «010» происходит при отказе резервного элемента с интенсивностью lр, переход «000» ® «002» происходит при ложном срабатывании переключателя с интенсивностью lл. Переходы «100» ® «110» и «010» ® «110» происходят при отказе основного или резервного элемента в режиме работы с интенсивностью l0. Переходы «010» ® «012» и «002» ® «012» происходят при отказе резервного элемента в режиме работы после ложного переключения на него или при ложном переключении на ранее отказавший резервный элемент соответственно с интенсивностью l0 или lл.
При восстановлении переходы происходят в обратном порядке. Переходы «100» ® «000», «010» ® «000», «002» ® «000» происходят при восстановлении одного элемента или переключателя с интенсивностью mв. Переходы «101» ® «000», «012» ® «000» тоже происходят с интенсивностью mв, так как по условию восстановление одного из элементов и переключателя происходит одновременно. Переход «110» ® «100» происходит с интенсивностью 2mв, так как по условию восстановление неограниченное и работает одновременно две бригады.
На основе графа по правилам, изложенным в п.2.2. легко составить систему уравнений Колмогорова, описывающую процесс отказов-восстановлений рассматриваемой системы.
 (4.31)
(4.31)
Для решения системы уравнений (4.31) из неё следует исключить любое одно уравнение, кроме последнего, представляющего собой нормирующее условие. В результате решения получаем вероятности всех состояний системы: p000, p100, p010, p002, p101, p012, p110.
По стационарным вероятностям состояний системы рассчитываются стационарные коэффициенты готовности, простоя и наработка между отказами
kг= 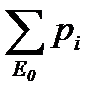 , kп=
, kп=  , T0=(1/kп-1)
, T0=(1/kп-1) 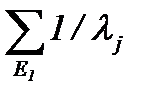 . (4.32)
. (4.32)
где pi – вероятность i – го состояния подмножества E0;
pj – вероятность j – го состояния подмножества E1;
lj – интенсивность выхода из j–го состояния подмножества E1.
В рассматриваемом нами случае
kг= p000+p100+p010+p002, kп= p101+p012+p110,
T0=(1/kп-1)(1/mв+1/mв +1/2mв) =(1/kп-1)×5/2mв.
Дата добавления: 2015-04-18; просмотров: 391; Мы поможем в написании вашей работы!; Нарушение авторских прав |