Выполнение работы. Как и в предыдущих задачах реализуем решение несколькими способами – непосредственно на листе, с помощью макроса и через функцию пользователя с получением

Как и в предыдущих задачах реализуем решение несколькими способами – непосредственно на листе, с помощью макроса и через функцию пользователя с получением значения интеграла.

Для этого открываем новую книгу Excel, сразу же переходим в редактор VBA (Ctrl+F11) и создаем там модельную функцию, интеграл которой будем вычислять.

Public Function My_Fun(x)

My_Fun = 150 + 5.2 * x - 0.75 * x ^ 2

End Function

Теперь на первом листе книги готовим традиционную таблицу, которая должна иметь заголовок, потом подзаголовки с указанием формулы для решения и непосредственно столбца, которые нужны для расчета по этим формулам (рис.5).

Как обычно отмечаем светло-зеленым фоном ячейки, которые требуют ввода данных. В ячейку с размером шага записываем формулу dH=(Xк-Xн)/k, где все параметры в формуле ссылаются на ячейки отмеченные фоном. В ячейки 4 строки надо вписать формулу суммы всех площадей сечений для каждой формулы, так для столбца «Е» имеет вид =СУММ(E7:E26).Число охваченных формулой ячеек должно быть равным или больше чем значение k. После ввода первой формулы, остальные можно просто скопировать на остальные ячейки строки.

Рис.5. Заголовок основной таблицы

Теперь начнем заполнять остальные ячейки формулами. В первую очередь заполняем номера сечений, для этого в первую ячейку вводим 1 (рис.6), а последующие ячейки по данному столбцу заполняем формулой =A7+1.

Начальное значение X приравниваем Xн, а далее по столбцу прибавляем к предыдущему значению вычисленный шаг (рис.7). Теперь надо заполнить остальные ячейки для первого сечения. Для средней точки сечения к начальному значению X прибавляем половину шага и для конечной точки прибавляем целый шаг (рис.8). Как видите, все ссылки на шаг имеют абсолютную адресацию (после ввода адреса фиксируем ячейку клавишей F4).

Теперь надо ввести формулы для вычисления площади сечения. Сами формулы показаны выше, а варианты их ввода в данные ячейки имеют следующий вид:

=My_Fun(B7)*$H$3

=My_Fun(D7)*$H$3

=My_Fun(C7)*$H$3

=(My_Fun(B7)+My_Fun(D7))/2*$H$3

=(My_Fun(B7)+4*My_Fun(C7)+My_Fun(D7))/6*$H$3

Теперь остается скопировать все формулы от Хс до 2д и вставить их в следующую строку, а потом данную строку растянуть до необходимого числа сечений. Полученный результат, показанный на рис.9.

Рис.9. Результат вычисления интеграла модельной функции.

Как видим, результаты вычислений достаточно близки, говорит ли это об одинаковой точности всех этих формул. Попробуем провести анализ точности наших результатов в зависимости от используемой формулы. Для этого построим график нашей функции и попробуем найти интегралы на разных ее участках. Сначала формируем таблицу данных для нашего графика (рис.10), где берем интервал изменения параметра «Х» от -8 до 15, а «Y» определяем по нашей модельной функции. Теперь по этим данным строим график (рис.11).

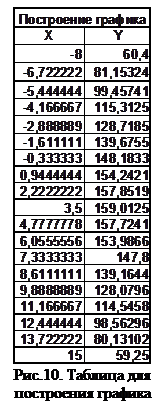
Рис.11. График модельной функции

Интерес на графике могут представлять три интервала – слева от экстремума, в районе экстремума и справа от него. Можно так же посмотреть влияние на погрешности ширины интервала в области экстремума. Построим новую таблицу, куда занесем результаты наших расчетов для различных областей (рис.12). Чтобы заполнить эту таблицу, сначала вводим заданный интервал в основную таблицу и потом копируем результаты расчета интегралов в соответствующие ячейки. Так как в исходных ячейках у нас находятся формулы сумм, то копирование должно выполняться командой «Специальная вставка» с выбором режима «Значения». Для представления данных стоит построить гистограмму, но лучше использовать не абсолютные значения интегралов, а их разности. В качестве наилучшего из методов возьмем результаты вычисления по формуле 2д и буде брать разности между этим значением и всеми другими. Получаем новую таблицу (рис.13). Формулы в ней имеют следующий вид – =B31-$F31.Как видим, ссылка на формулу 2д имеет символ доллара пере именем столбца «F», что делает данный адрес абсолютно-относительным. Столбец будет закреплен, что позволит просто скопировать все формулы сначала по строке, а потом все ячейки по столбцам.

Построим гистограмму (рис.14). Как видно из гистограммы в интервале, где имеет место нарастание функции (положительная производная) первая формула существенно занижает значение интеграла, а вторая формула наоборот. Вычисления интегралов в области экстремумов выравнивает эти погрешности, но здесь возрастают ошибки третьей и четвертой формул. Если нет проблем с дополнительными вычислениями функции, то лучше пользоваться последней формулой.

Теперь реализуем эту же задачу средствами VBA – создадим непосредственно функцию пользователя, которая сразу же возвращает значение интеграла. Сначала поставим задачу:

− входными параметрами в программе должны быть границы интервала, точность решения, имя функции, которая используется в решении и номер формулы, которую будем использовать в расчетах;

− реализуем алгоритм, показанный на рис.4;

− для вычисления площади сечения создадим внутреннюю подпрограмму-функцию, которая на основании значений начальной точки сечения, шага, имени функции и номера формулы вычисляет площадь;

Переходим в редактор VBA и в модуле создаем функцию «Integral». Вводим формальные параметры в заголовок функции и заполняем собственно тело программы:

Public Function Integral(xn, xk, Fn As String, _

N_form, erf, Show As Boolean)

If erf = 0 Then erf = 0.01

k = 10: h = (xk - xn) / k

s = 0: xt = xn

For i = 1 To k

s = s + GetFun(xt, h, Fn, N_form)

xt = xt + h

Next i

Do

k = k * 2: h = (xk - xn) / k

s1 = 0: xt = xn

For i = 1 To k

s1 = s1 + GetFun(xt, h, Fn, N_form)

xt = xt + h

Next i

If Abs(s1 - s) < erf Then Exit Do

s = s1

Loop

If Show Then

MsgBox "Заданная точность достигнута при k=" & k, _

vbInformation + vbOKOnly

End If

Integral = s1

End Function

Разберем программу более подробно. В первой строке проверяем задание точности вычисления для исключения ошибок при запуске программы. Потом задаем начальное значение k=10, вычисляем dH, обнуляем S и задаем Xt=Xн. В цикле от 1 до k суммируем площади сечений, обращаясь в внутренней функции GetFun и изменяем Xt. После организуем бесконечный цикл вычисления следующего значения интеграла в переменную S1, повторяя только, что описанные строки. Получив второе значение интеграла, проверяем условие достижения заданной точности в операторе If. При достижении заданного условия реализуем выход из цикла, иначе сохраняем значение S1 в S и повторяем вычисление интеграла еще раз. Для анализа скорости получения решения перед выходом из функции ставим вывод служебного окно (MsgBox) с сообщение числа k, при котором найдено решение. Если мы оставим это сообщение постоянно, то нам придется после каждого вычисления нажимать «Ok». Чтобы можно было управлять выводом этой информации внесем еще один формальный параметр «Show» как логическая переменная, которая может принимать два значения «ИСТИНА» и «ЛОЖЬ». Заключаем оператор с выводом окна в условный оператор «If». Теперь если переменная «Show» принимает значение «ИСТИНА», то вспомогательное окно выводится на экран.

Формируем программу вычисления площади «GetFun»:

Private Function GetFun(XX, dH, Fn, N)

Select Case N

Case 1

Y1 = Application.Run(Fn, XX)

Y = Y1 * dH

Case 2

Y1 = Application.Run(Fn, XX + dH)

Y = Y1 * dH

Case 3

Y1 = Application.Run(Fn, XX + 0.5 * dH)

Y = Y1 * dH

Case 4

Y1 = Application.Run(Fn, XX)

Y2 = Application.Run(Fn, XX + dH)

Y = (Y1 + Y2) / 2 * dH

Case 5

Y1 = Application.Run(Fn, XX)

Y2 = Application.Run(Fn, XX + dH)

Y3 = Application.Run(Fn, XX + dH / 2)

Y = (Y1 + Y3 * 4 + Y2) / 6 * dH

End Select

GetFun = Y

End Function

Теперь можем проверить работоспособность наших подпрограмм. На листе Excel подготовим табличку для вычисления интеграла модельной функции через разные формулы с различной точностью. Вносим заголовок таблицы и готовим комментарии к переменным, которые надо будет передавать для вычисления интеграла в функцию (рис.15). Как и ранее все ячейки с исходными данными окрашиваем светло-зеленым фоном. В ячейки строки «Интеграл» записываем формулу – =Integral($B$44;$D$44;$B$45;B46;$D$45;$F$43). Все фактические параметры имеют абсолютные адреса кроме номера формулы, который берется из ячейки сверху. Строку «k» можно заполнить вручную, если поставить в ячейку «Показать число k» значение «ИСТИНА» или «True». Программа выполнить расчет всех ячеек и выведет пять раз окно с информацией (рис.16).

Заключение

В результате выполнения работы были разработаны программы для вычисления интеграла с использованием различных квадратурных формул. Выполнен анализ точности расчетов по каждой из формул. Создана функция пользователя, которая может быть использована в расчетах, когда надо будет вычислять интегралы.