Правило 3

Если F(x) есть некоторая первообразная для функции f(x), а k и b есть некоторые постоянные, причем k не равняется нулю, тогда (1/k)*F*(k*x+b) будет первообразной для функции f(k*x+b).

Данное правило следует из правила вычисления производной сложной функции:

((1/k)*F*(k*x+b))’ = (1/k)*F’(k*x+b)*k = f(k*x+b).

Приближённое нахождение первообразных(метод Эйлера)

Пусть на интервале 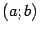задана непрерывная функция 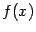, для которой нужно найти первообразную . Согласно определению первообразной, для этого нужно решить уравнение

(1.6)

найдя неизвестную функцию . Относительно этой неизвестной функции уравнение является дифференциальным уравнением первого порядка. Его можно приближённо решать разными способами, которые вы будете изучать в курсе дифференциальных уравнений. Опишем здесь простейший из них, называемый методом Эйлера.

Из всего семейства первообразных 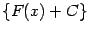будем отыскивать ту первообразную, которая в некоторой фиксированной точке 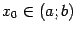принимает фиксированное значение 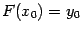. Это условие выделяет из семейства первообразных одну функцию: все остальные первообразные 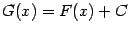отличаются от этой фиксированной первообразной на постоянное слагаемое и, следовательно, не удовлетворяют условию .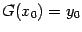

Заметим, что из уравнения (1.6) следует, что

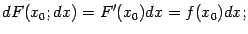
найденный дифференциал равен главной линейной части приращения функции:

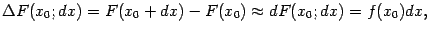
откуда

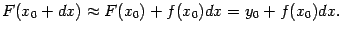
Здесь мы учли начальное условие 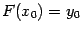. Тем самым, взяв некоторое приращение независимого переменного , равное , мы сможем приближённо найти значение первообразной в "соседней" точке :

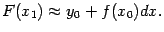
Начав аналогичные вычисления с точки 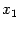вместо 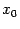, получаем

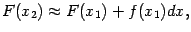
где 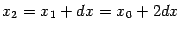; затем точно так же получаем

где , и т. д. По найденным в известных точках , , 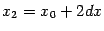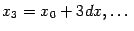приближённым значениям первообразной мы можем построить график функции (разумеется, приближённо, поскольку значения известны лишь приближённо). Выбирая 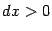, мы построим этот график при 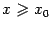, то есть на 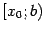, а повторив процесс при , построим часть графика на .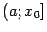

Заметим, что шаг по оси , то есть величину , не обязательно выбирать одинаковым на всех этапах: 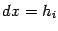может зависеть от номера этапа 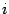. Рекомендуется учитывать при этом выборе поведение функции 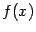и уменьшать шаг 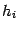, если значения 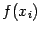увеличиваются, и увеличивать 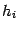, если значения 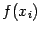уменьшаются, чтобы величины приращений 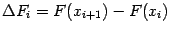были бы примерно одинаковы по абсолютной величине. Это даст возможность более точно построить график первообразной .