Виды резервирования систем. Постановка задачи оптимального резервирования. Подходы к решению задачи оптимального резервирования.

Резервирование - способ повышения надежности @ путем включения в её состав резерва, предусмотренного на стадии проектирования этой системы или во время эксплуатации.

Рез-ние замещением: при отказе эл-та, @ перестраивается, и в замен отказавшего подключается эл-т из числа резервных.

Автоматическое: при отказе основного эл-та автоматически подкл-ся резервный. Постоянное: резервные и основные эл-ты нах-ся в одинаковых усл и параллельно выполняют заданные ф-ии. Общее: резервируется вся система в целом.

Раздельное: резервируются отдельные участки @. Скользящее: один резервный эл-т предназначен для рез-ния некот. множества основных эл-в такого же типа. При отказе он заменяется. Нагруженное: резервные эл-ты @ нах-ся во вкл. состоянии, работают параллельно с основными эл-ми и практически одинаково расходуют свой ресурс работы. Ненагруженное: резервные эл-ты нах-ся в выкл-ом состоянии и практически не расходуют свой ресурс работы. Облегченное: резервные эл-ты нах-ся во вкл состоянии, однако расходуют свой ресурс намного меньше, чем при подключении их на место основных.

Постановка задачи оптимального резервирования ИС состоят из отдельных эл-тов, которые с течением времени отказывают и заменяются резервными. Снятые с эксплуатации эл-ты подвергаются ремонту. Модель должна определять оптимальный уровень резервных эл-тов каждого типа. По условию задачи требуется, чтобы @ функционировала с максимальной надежностью. Если какой-нибудь эл-т отказывает, то его заменяют запасным из числа резервных. Отказавший эл-т сразу начинают ремонтировать. В @ непрерывно должно функционировать zk элементов k-гo типа, причем в запасе должно иметься xk элементов того же k-го типа k=(1,2,...,S). Сущность задачи заключается в оптимальном распределении стоимостных или каких-либо других ресурсов С₀, выделенных на приобретение резервных единиц. Рассм-ая. @ считается отказавшей, если в момент отказа работающего элемента k-го типа все хk запасных эл-в того же типа находятся в ремонте. Т.о., надо найти такое кол-во резервных эл-в={x_l,x₁,x₃,..,x_k}, чтобы вероятность нехватки рез-х эл-в была мин-ой. Введем обозначения:

Р( ) - показатель надёжности всей системы (вероятность безотказной работы системы); P_k(X_k) - вероятность безотказной работы k-гo элемента. Так как модель соединений эл-в, с точки зрения надежности, представляется как последовательное соединение эл-в, то справедлива формула:

На все эл-ты есть ограничения (вес, цена, объем и т д), Но мы будем пользоваться только стоимостным ограничением как, где С_k - стоимость одного элемента k-гo типа. Для решения задачи оптимального резервирования используется прежде всего метод динамического программирования. В основе метода лежит пошаговый процесс, на каждом шаге строится доминирующая последовательность {[Q(X₁), C(X₁)], [Q(X₂),C(X₂)]} где переход в состояние с более высокой надежностью (или более низкой вероятностью отказа Q) происходит с минимальными затратами по стоимости С, здесь Q( )=1-Р( ) есть риск нехватки резервных элементов. Доминирующая последовательность строится по правилу: 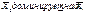, если Алгоритм построения доминирующей последовательности состоит из шагов, на каждом из которых строится таблица. Рассматриваем две подсистемы из 1-го и 2-го типов элементов. Характеристики элементов 1-го типа записываются в заголовках столбцов, а характеристики 2-го типа - в заголовках строк. На пересечении каждой строки и каждого столбца записываются суммы стоимостей С и вероятностей нехватки элементов q (табл.). Вначале проводим анализ элементов таблицы по ограничениям. Вычеркиваем те элементы, которые имеют значение стоимости большее, чем ограничение по стоимости С₀ и ограничение по вероятности нехватки элементов Q₀. Делаем анализ на доминирование: рассматриваем оставшиеся клетки и сравниваем последовательно со всеми элементами (клетками). Если для каких-то двух векторов выполняется условие строгого доминирования, тогда худший вычеркивается. Вектор X₁ доминирует над вектором Х₂, если вероятность нехватки элементов Р(Х₁)≥Р(Х₂), а стоимость C(X₁)≤С(Х₂)(ЗАДАЧА НА МАХ), или вероятность нехватки элементов. Q(X₁)≤Q(Х₂) и стоимость С(X₁)≤С(Х₂)(ЗАДАЧА НА MIN). Вектор X₁ строго доминирует над вектором Х_2, если одно из перечисленных неравенств будет строгим. Все оставшиеся элементы переносим в заголовки столбцов, а в заголовках строк будут характеристики элементов третьего типа. Всего будет S-1 таблица(где S-кол-во эл-тов @), на последнем шаге вычислений ищется оптимальный вектор, у которого и будет минимальная вероятность отсутствия резервных элементов. Т.о. получаем оптимальный состав устройств.

Также используется метод неопределенных множеств Лагранжа.