Смешанное решение матричной игры.

Теория игр – часть обширной теории, кот занимается оптимальными решениями рассм. Обычно конфликтные ситуации.Конфл-ые ситуации – это ситуации реш-е в кот оптимальное для одной стороны, не явл таковым для др, а рез-т зависит от всех конфл-х сторон. Игра – всякая конфл. ситуация рассм в теории игр и предст собой упрощенную модель ситуации. Стратегия- это доступные для игроков действия, в общем случае набор правил ограничений. Ситуация – возможные исходы конфликта. Каждая ситуация рез-т выбора игроком своей стратегии. Игра наз игрой с нулевой суммой(антогонистической), если она парная и выигрыш одного из игроков равен проигрышу другого.Антогонистическая игра в кот. каждый игрок имеет конечное мн-во стратегий наз. матричной. Соотв-но решить игру или найти решение игры, значит для каждого игрока найти стратегию, кот. уд-ет усл. оптимальности: Один из игроков должен получить максимальный выигрыш, когда второй придерживается своей стратегии. В то же время 2-ой должен иметь минимальный проигрыш, если 1-ый игрок придерживается своей стратегии. Такие стратегии нез оптимальными. Условие устойчивости: каждому игроку не выгодно отступать от оптимальных стратегий.

Платёжной матрицей игры – наз матрица эл-ми кот явл. Выигрыши, соответствующие разл стратегиям 2-х игроков.

Нижняя цена игры или максимин:

=4

Верхняя цена игры или минимакс . =4

Оптимальные стратегии: =(0,1,0), =(0,0,1)

Задачи в кот. минимакс равен максимину имеют седловую точку. Говорят также игра имеет решение в чистых стратегиях. . Если в игре нет Седловой точки, то решение в чистых стратегиях не существует.

Смешанной стратегией игрока A наз применение его чистых стратегий с вероятностью

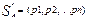. Причем . Соответственно для игрока В: ; ;

На основании принципа минимакса опр-ся оптимальное решение игры: это пара оптимальных стратегий в общем случае смешанных, обладающих след св-вом: Если один из игроков придерживается своей оптим-о й стратегии, то другому не выгодно отступать от своих. При этом выигрыш соотв-щий оптим-му решению наз ценой игры, кот уд-ет нер-ву: .

Основная теорема ТИ (теорема фон Неймана): каждая конечная игра имеет по крайней мере 1 решение (возможно в области смешанных стратегий). Выигрыш, полученный в результате решения, называется ценой игры. След., каждая конечная игра имеет цену. Цена игры лежит всегда между нижней и верхней ценой игры:

Игра 2*2 явл. простейшим случаем конечной игры. Если такая игра имеет седловую точку, то оптимальное решение – это пара чистых стратегий, соотв-щих этой точке. Игра, в кот отсутствует седловая точка в соотв-ии с основной теоремой теории игр, имеет оптим-е решение и опр-ся парой смешанных стратегий: и .

Пусть игра задана платёжной матрицей A. Если мы придерживаемся своей опт. стратегии S_a^*, то противник может пользоваться любой из своих стратегий В₁, В₂, не изменяя сред. выигрыша υ. Отсюда имеем 2 ур-я:

а₁₁p₁+a₂₁p₂=n - наша стратегия S_a^* и стратегия противника В₁

а₁₂p₁+a₂₂p₂=n - наша стратегия S_a^* и стратегия противника В₂

Т.к. p₁+p₂ = 1, выражаем p₁= 1 - p₂.

Получаем Отсюда выражаем p₂. Подставляем их значения в одно из уравнений системы – получаем цену игры υ.

Если υ известна, то для определения оптим. стратегии противника S_в^* нам достаточно одного уравнения:

а₁₁q₁+a₂₁q₂=n. Получаем: q₁ = (υ – a₁₂)/(a₁₁ – a₁₂). Выражаем q₂=1- q₁. Получаем оптимальную стратегию S_в^*.

Надежность, эргономика и качество АСОИУ/Надежность ИС