Система с последовательным соединением элементов

Самым простым случаем в расчетном смысле является последовательное соединение элементов системы. В такой системе отказ любого элемента равносилен отказу системы в целом. По аналогии с цепочкой последовательно соединенных проводников, обрыв каждого из которых равносилен размыканию всей цепи, мы и называем такое соединение "последовательным" (рис. 1). Следует пояснить, что "последовательным" такое соединение элементов является только в смысле надежности, физически они могут быть соединены как угодно.

Рис. 1. Блок-схема системы с последовательным соединением элементов

С позиции надежности, такое соединение означает, что отказ устройства, состоящего из этих элементов, происходит при отказе элемента 1 или элемента 2, или элемента 3, или элемента n. Условие работоспособности можно сформулировать следующим образом: устройство работоспособно, если работоспособен элемент 1 и элемент 2, и элемент 3, и элемент n.

Выразим надежность данной системы через надежности ее элементов. Пусть имеется некоторый промежуток времени (0,t), в течение которого требуется обеспечить безотказную работу системы. Тогда, если надежность системы характеризуется законом надежности Р(t), нам важно знать значение этой надежности при t=t, т.е. Р(t). Это не функция, а определенное число; отбросим аргумент t и обозначим надежность системы просто Р. Аналогично обозначим надежности отдельных элементов P₁, P₂, P₃, ..., P_n.

Для безотказной работы простой системы в течение времени t нужно, чтобы безотказно работал каждый из ее элементов. Обозначим S - событие, состоящее в безотказной работе системы за время t; s₁, s₂, s₃, ..., s_n - события, состоящие в безотказной работе соответствующих элементов. Событие S есть произведение (совмещение) событий s₁, s₂, s₃, ..., s_n: S = s₁×s₂×s₃×...×s_n.

Предположим, что элементы s₁, s₂, s₃, ..., s_n отказывают независимо друг от друга (или, как говорят применительно к надежности, "независимы по отказам", а совсем кратко "независимы"). Тогда по правилу умножения вероятностей для независимых событий Р(S)=P(s₁)×P(s₂)×P(s₃)×...×P(s_n) или в других обозначениях,

Р = Р₁×Р₂×Р₃×...×Р_n., (1)

а короче P = 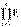, (2)

Т.е. надежность (вероятность работоспособного состояния) простой системы, составленной из независимых по отказам, последовательно соединенных элементов, равна произведению надежностей ее элементов.

В частном случае, когда все элементы обладают одинаковой надежностью P₁=P₂=P₃= ... =P_n, выражение (2) принимает вид

Р = Pⁿ. (3)