Реактор в форме параллелепипеда

Рассматривается активная зона в форме прямоугольного бруса с длинами сторон соответственно a, b и c. Для трехмерной прямоугольной геометрии уравнение Гельмгольца

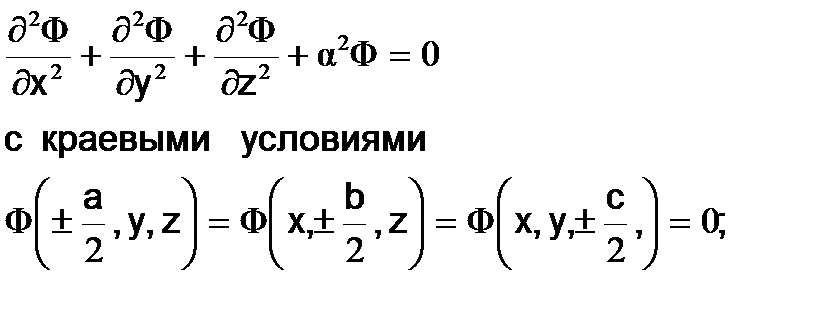
Применяя к этой задаче метод разделения переменных

2

преобразуем исходное уравнение в систему трех обычных дифференциальных уравнений

решение каждого из которых аналогично решению для одномерной пластины. С учетом граничных условий общее решение для прямоугольного параллелепипеда запишем в виде

Критическое условие принимает вид

Сравним между собой минимальные критические размеры реакторов различных геометрических форм для одной и той же размножающей среды, характеризующейся материальным параметром c². Для реактора сферической формы

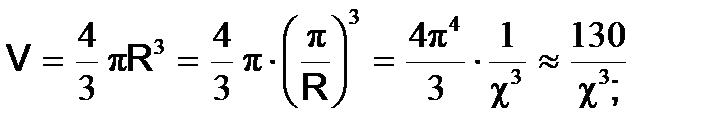
Для конечного цилиндра и прямоугольного параллелепипеда критическое условие 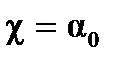может выполняться при различных соотношениях между радиусом и высотой цилиндра или сторонами параллелепипеда, а, следовательно, при разных объемах.

Найдем оптимальное соотношение между высотой и радиусом цилиндра, исходя из условия минимальности критического объема. Математически задача формулируется следующим образом:

Из условия критичности выразим R² как функцию H и подставим в выражение для объема цилиндра. В результате мы сведем исходную задачу с двумя переменными к задаче на минимум функции одной переменной, а именно, высоты реактора. Для этой задачи условие минимальности формулируется обычным образом.

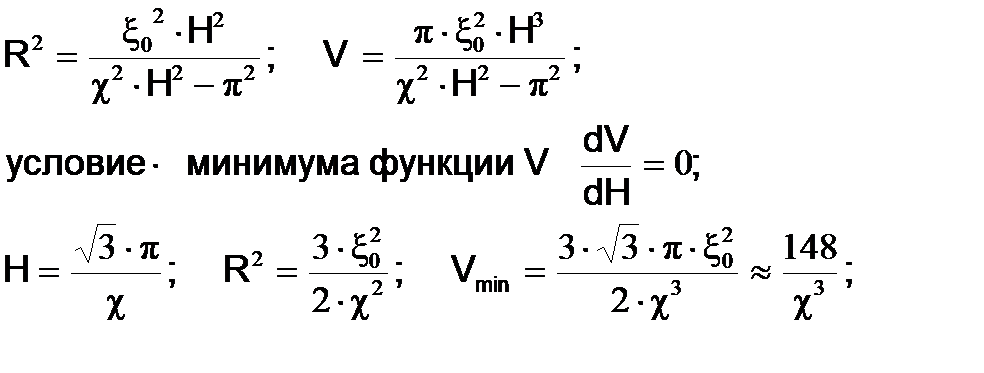
Довольно очевидно, что для прямоугольного параллелепипеда условие оптимальности размеров дается соотношением a=b=c (условие симметрии), а минимальный критический объем имеет куб, для которого

Итак, можно записать отношение минимальных объемов шара, куба и цилиндра при заданном материальном параметре размножающей среды c