
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Управление ядерным реактором. Роль запаздывающих нейтронов в управляемых нестационарных процессах. Возникновение и отличие в свойствах мгновенных и запаздывающих нейтронов.
Ряд нуклидов, образующихся в результате деления тяжёлых ядер (изотопы брома, йода, ксенона, криптона, цезия и др.), оказываются пересыщенными нейтронами и испускают избыточные нейтроны в результате радиоактивного распада с периодами, существенно превышающими время жизни мгновенных нейтронов, от долей секунды до десятков секунд. Относительная доля запаздывающих нейтронов невелика, существенно меньше 1%, и зависит от типа разделившегося ядра. В таблице 2.2.1 приведены относительные выходы запаздывающих нейтронов при делении тепловыми нейтронами для основных делящихся нуклидов.
Таблица 2.2.1
| Нуклид | 233U | 235U | 239Pu | 241Pu |
| Выход запаздывающих | 0,00266 | 0,0065 | 0,00212 | 0,0053 |
| нейтронов, b | (0,266 %) | (0,65%) | (0,21%) | (0,53%) |
Поскольку число ядер-эмиттеров запаздывающих нейтронов довольно велико, и они имеют большой диапазон характерных времён жизни (периодов полураспада), для решения практических задач ядра-эмиттеры объединяют в группы с близкими по величине периодами.
Имеются незначительные отличия в групповых характеристиках ядер-эмиттеров для других делящихся нуклидов, а также при делении быстрыми нейтронами. Нуклиды уран-238 и торий-232 делятся только быстрыми (надпороговыми) нейтронами. Выход запаздывающих нейтронов для этих нуклидов составляет, соответственно, 1,61 и 2,28%.
Главная особенность запаздывающих нейтронов состоит в том, что они рождаются в результате радиоактивного распада ядер-эмиттеров, и их средняя энергия при рождении существенно ниже, чем у мгновенных нейтронов. Если у мгновенных нейтронов средняя энергия составляет около 2 Мэв, то у запаздывающих она порядка 0,5 Мэв. Это означает, что запаздывающие нейтроны не могут вызвать деление нуклидов с пороговым сечением, урана-238 и тория-232. С другой стороны, запаздывающие нейтроны, имея более низкую энергию, имеют несколько большую вероятность избежать утечки при замедлении. Эти особенности должны учитываться при анализе процессов с участием запаздывающих нейтронов.
Среднее время жизни ядер-эмиттеров в стационарном режиме, а по существу - среднее время запаздывания при рождении запаздывающих нейтронов равно 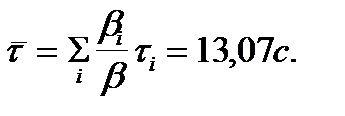 Соответственно, средняя величина постоянной распада
Соответственно, средняя величина постоянной распада 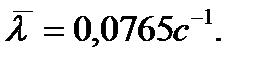
20. Кинетика реактора на примере "точечной" модели с одной группой эмиттеров запаздывающих нейтронов. Связь периода реактора с реактивностью.
Простейшей моделью для анализа нестационарных процессов в реакторе является модель с одной эффективной группой эмиттеров запаздывающих нейтронов без внешнего источника. Суть модели состоит в том, что всем эмиттерам запаздывающих нейтронов приписывается одинаковое осреднённое значение постоянной распада 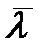 (или время жизни
(или время жизни  ). Тогда полная концентрация ядер-эмиттеров есть
). Тогда полная концентрация ядер-эмиттеров есть  . В качестве первого приближения осреднённой величины постоянной распада
. В качестве первого приближения осреднённой величины постоянной распада 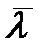 можно принять величину, соответствующую стационарному состоянию
можно принять величину, соответствующую стационарному состоянию 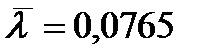 . Далее знак осреднения будем опускать. Модель кинетики в этом приближении сводится к системе двух уравнений:
. Далее знак осреднения будем опускать. Модель кинетики в этом приближении сводится к системе двух уравнений:
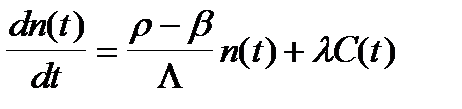
(2.4.1)
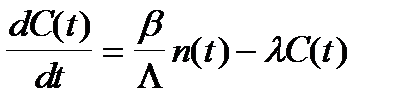 .
.
Не претендуя на адекватное количественное описание нестационарных процессов, модель с одной группой эмиттеров даёт возможность в ряде случаев получить аналитические решения, отражающие их основные качественные особенности.
Предположим, что до момента t=0 реактор находился в стационарном состоянии: r=0; 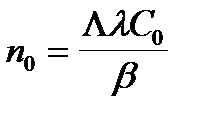 . В момент t=0 реактивность изменяется скачкообразно и принимает некоторое постоянное значение r. Систему уравнений (2.4.1) в этом случае можно характеризовать как систему линейных однородных уравнений с постоянными коэффициентами. Общее решение такой системы может быть представлено суперпозицией двух (по числу уравнений) экспонент типа
. В момент t=0 реактивность изменяется скачкообразно и принимает некоторое постоянное значение r. Систему уравнений (2.4.1) в этом случае можно характеризовать как систему линейных однородных уравнений с постоянными коэффициентами. Общее решение такой системы может быть представлено суперпозицией двух (по числу уравнений) экспонент типа 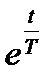 , периоды которых могут быть найдены из соответствующего характеристического уравнения, а коэффициенты перед экспонентами - из начальных условий. Подставив общее решение в систему (2.4.1) и учитывая , что
, периоды которых могут быть найдены из соответствующего характеристического уравнения, а коэффициенты перед экспонентами - из начальных условий. Подставив общее решение в систему (2.4.1) и учитывая , что 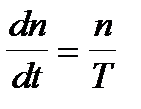 ,
,
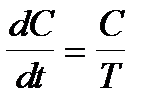 , легко получить характеристическое уравнение, связывающее периоды с введенной реактивностью:
, легко получить характеристическое уравнение, связывающее периоды с введенной реактивностью:
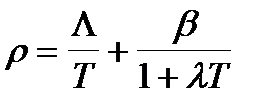 . (2.4.2)
. (2.4.2)
Уравнение (2.4.2) носит название уравнения “обратных часов” и в модели с одной группой эмиттеров является уравнением 2-го порядка относительно Т. Прежде чем искать корни уравнения (2.4.2), полезно провести общий качественный анализ взаимной зависимости r и Т. Соответствующая качественная зависимость представлена на рис. 2.4.1.
Как видно из рисунка, при Т>0 чем меньше реактивность r, тем больше период Т, и наоборот, уменьшение периода соответствует росту реактивности. При Т=0 имеет место разрыв в зависимости r(Т), и при Т<0 r изменяется от -¥ до +¥ в диапазоне 0>T> - 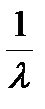 . При
. При
Т= - 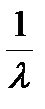 имеет место следующий разрыв, и при Т< -
имеет место следующий разрыв, и при Т< - 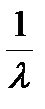 функция r(Т) везде отрицательна и монотонно стремится к 0 с ростом Т по абсолютной величине. Таким образом, при постоянной реактивности любого знака, из двух корней Т1,2 характеристического уравнения (2.4.2) один корень имеет знак введенной реактивности, а второй корень всегда отрицателен и локализован в интервале 0>Т> -
функция r(Т) везде отрицательна и монотонно стремится к 0 с ростом Т по абсолютной величине. Таким образом, при постоянной реактивности любого знака, из двух корней Т1,2 характеристического уравнения (2.4.2) один корень имеет знак введенной реактивности, а второй корень всегда отрицателен и локализован в интервале 0>Т> - 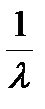 .
.
Период, соответствующий первому корню, носит название асимптотического периода и характеризует нестационарный процесс при больших временах. Второй, отрицательный период характеризует быстро затухающую составляющую нестационарного процесса.
Рис.2.4.1. Связь между периодом и реактивностью в модели c одной группой эмиттеров запаздывающих нейтронов.
Второе важное замечание: при любой величине отрицательной реактивности соответствующий асимптотический период не может быть по абсолютной величине меньше, чем 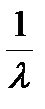 , то-есть меньше , чем время жизни эмиттеров запаздывающих нейтронов.
, то-есть меньше , чем время жизни эмиттеров запаздывающих нейтронов.
Количественные значения периодов Т1,2 могут быть получены из характеристического уравнения (2.4.2), преобразованного к форме квадратного уравнения относительно Т:
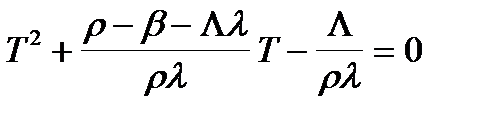 . (2.4.3)
. (2.4.3)
 (2.4.4)
(2.4.4)
Учитывая, что время генерации L »10-3 - 10-6 с, а постоянная распада l»10-1 с-1, произведение Ll обычно существенно меньше b. Если введенная положительная реактивность r<<b, либо реактивность отрицательная, произведением Ll в (2.4.4) можно пренебречь. В этом случае можно получить приближённые значения периодов Т1,2 :
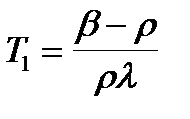 (2.4.5)
(2.4.5)
 (2.4.6)
(2.4.6)
Судя по полученным выражениям, асимптотический период Т1 соразмерен времени жизни эмиттеров запаздывающих нейтронов 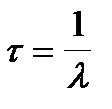 , в то время как переходный период Т2 соразмерен времени генерации, или времени жизни мгновенных нейтронов L.
, в то время как переходный период Т2 соразмерен времени генерации, или времени жизни мгновенных нейтронов L.
Решение уравнения (2.4.1) для плотности нейтронов, удовлетворяющее начальным условиям, можно представить в виде:
 (2.4.7)
(2.4.7)
Легко убедиться, что при t=0 выполняется начальное условие: n(0)=n0 .Представление о качественном характере зависимости n(t) и её составляющих при положительном и отрицательном скачке реактивности даёт рис 2.4.2, а, б.
а) Положительный б) Отрицательный
скачок r скачок r
Рис. 2.4.2. Зависимость плотности нейтронов от времени в модели с одной группой эмиттеров запаздывающих нейтронов.
Из приведенных на рис.2.4.2 графиков видно, что после введения скачка реактивности в реакторе формируется быстрый переходный процесс, приводящий к увеличению или уменьшению плотности нейтронов, в зависимости от знака введенной реактивности, завершающийся экспоненциальным нарастанием либо падением плотности нейтронов с характерным асимптотическим периодом. При этом первое слагаемое в (2.4.7) формирует асимптотическую составляющую n(t), а второе слагаемое описывает быстрый переходный процесс и обеспечивает непрерывность решения. В реальном диапазоне возможных изменений реактивности, не приводящих к разгону на мгновенных нейтронах, переходный период Т2 составляет доли секунды. Например, если введенная положительная реактивность r<<b, то, при времени генерации
L=10-4 с и b=0,0065 переходный период Т2»1,5*10-2с. При таком периоде слагаемое, описывающее переходный процесс, уменьшается в 100 раз через время порядка 0,07 с. Если в прикладных задачах рассматриваются процессы спустя значительно большие времена, вторым слагаемым в (2.4.7) можно пренебречь. Тогда решение, описывающее только асимптотическое поведение n(t), примет вид:
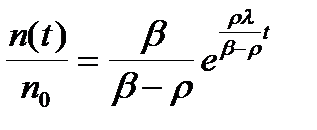 . (2.4.7a)
. (2.4.7a)
Обратимся теперь к зависимости от времени концентрации эмиттеров запаздывающих нейтронов C(t). Формально общее решение C(t) есть комбинация экспонент с теми же периодами Т1 и Т2, но с другими коэффициентами, соответствующими начальным условиям для эмиттеров. Однако можно показать, что в рамках принятых допущений относительно соотношения между Ll и |b-r| коэффициент перед экспонентой с переходным периодом обращается в ноль, и зависимость C(t) может быть представлена в виде:
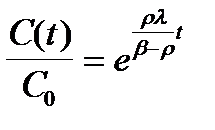 . (2.4.8)
. (2.4.8)
Таким образом, асимптотическое поведение и плотности нейтронов, и концентрации эмиттеров совершенно подобно и описывается одной экспонентой с асимптотическим периодом Т1. Существенная разница во временной зависимости плотности нейтронов и эмиттеров имеет место только в начальный момент, до формирования асимптотического режима, и это находит простое объяснение. Мгновенные нейтроны, появляющиеся в акте деления и имеющие малое время жизни, практически мгновенно реагируют на изменение баланса цепной реакции и способны изменить свою плотность за очень малое время. С другой стороны, эмиттеры запаздывающих нейтронов представляют собой материальную субстанцию с существенно большим временем жизни по сравнению с мгновенными нейтронами. Их накопление и распад не могут произойти скачкообразно. Поскольку эмиттеры запаздывающих нейтронов образуются в результате реакции деления, а плотность реакции деления, пропорциональная плотности нейтронов, сама определяется концентрацией эмиттеров, то рано или поздно устанавливается режим, при котором и плотность нейтронов, и концентрация эмиттеров согласуются между собой и подчиняются единому закону изменения во времени. В модели с одной группой эмиттеров этот режим наступает спустя доли секунды после изменения реактивности.
Обратим внимание на выражение (2.4.5) для асимптотического периода Т1. Поделив числитель и знаменатель этого выражения на b, получим следующий результат:
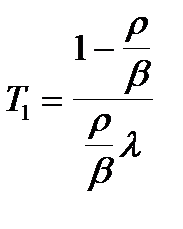 (2.4.5a)
(2.4.5a)
Это выражение, связывающее асимптотический период с относительной величиной реактивности, в единицах b, более удобно для прикладных задач, в частности, для интерпретации результатов экспериментов по определению “веса” регулирующих стержней, в условиях, когда величина эффективной доли запаздывающих нейтронов точно неизвестна. Соответствующее выражение для 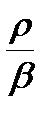 имеет вид:
имеет вид:
 . (2.4.9)
. (2.4.9)
Легко заметить, что формула (2.4.9) может быть получена из уравнения “обратных часов” (2.4.2), если время генерации положить равным нулю.
Заметим, что во всех официальных документах, регламентирующих условия управления и безопасности реакторов, используется относительная величина реактивности 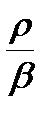 , поскольку именно она предопределяет характер и скорость нестационарных процессов независимо от абсолютной величины b. Естественно, чем меньше абсолютная величина b, тем меньше диапазон абсолютных изменений реактивности, обеспечивающих управление реактором в безопасных пределах.
, поскольку именно она предопределяет характер и скорость нестационарных процессов независимо от абсолютной величины b. Естественно, чем меньше абсолютная величина b, тем меньше диапазон абсолютных изменений реактивности, обеспечивающих управление реактором в безопасных пределах.
Как видно из выражения (2.4.9), при определении “веса” регуляторов, либо изменений реактивности, связанных с другими возмущениями размножающих свойств реактора, по асимптотическому периоду точность количественной оценки относительной реактивности зависит от величины постоянной распада эмиттеров l. Ниже будет показано, что постоянная распада l сама зависит от величины введенной реактивности и определяется относительным вкладом групп эмиттеров в полную эмиссию запаздывающих нейтронов.
Дата добавления: 2015-04-18; просмотров: 567; Мы поможем в написании вашей работы!; Нарушение авторских прав |