Амплитудно-модулированные колебания.

Амплитудная модуляция является наиболее простым и очень рас­пространенным в радиотехнике способом заложения информации в вы­сокочастотное колебание. При амплитудной модуляции огибающая амплитуд несущего колебания изменяется по закону, совпадающему с изменением передаваемого сообщения, частота же и начальная фаза колебания поддерживаются неизменными. Поэтому для амплитудно-модулированного радиосигнала можно общее выражение имеет вид:

(1.1)

Характер огибающей A(f) определяется видом передаваемого сооб­щения. При непрерывном сообщении (рис.1, а)модулированное колеба­ние приобретает вид, показанный на рис.1,б.

Огибающая A(t) изменяется по закону, воспроизводящему сообщение s(t). Рис.1,б построен в предположении, что постоянная составляющая функции S{t) равна нулю (в противоположном случае A₀ может не совпадать с амплитудой немодулированного колебания). Наибольшее изменение A(t) «вниз» не может быть больше амплитуды несущего колебания А₀. Изменение же «вверх» может быть в принципе и больше A₀

Для сохранения формы сообщения максимальное изменение A(t) не должно по абсолютной, величине превышать А₀. Это означает, что глубина модуляции амплитуды не должна превышать 100%.

Определение понятия «глубина модуляции» особенно наглядно для случая тональной модуляции, когда модулирующая функция s(t) является гармоническим колебанием: (1.2)

Огибающая модулированного колебания при этом может быть за­писана в виде (1.3)

где Ω — частота модулирующей функции; γ — начальная фаза оги­бающей; k—-коэффициент пропорциональности; ΔAm = kS₀ — ам­плитуда изменения огибающей (рис.2).

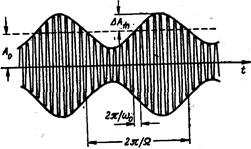Отношение M = ΔAm/A₀ называется коэффициентом глубины модуляции или просто коэффициентом модуляции.

Таким образом, мгновенное значение модулированного колебания можно записать в форме (1.4)

При неискаженной модуляции (М ≤ 1) амплитуда колебания из­меняется в пределах от минималной А_мин = А₀(1-М) до максималь­ной А_макс = А₀(1 +М)