Аналитический сигнал. Свойства сопряженных по Гильберту сигналов.

В электротехнике общепринято представлять гармоническое коле­бание (ток, напряжение) в форме

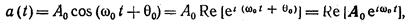(1.1)

(1.2)

где —комплексная амплитуда.

Часто символы Re или Im опускают и пишут просто

(1.3)

подразумевая действительную или мнимую часть этого выражения.

В современной радиотехнике представление колебаний в комплексной форме получило дальнейшее развитие и распространено на негармонические колебания.

Если задан «физический» сигнал в виде действительной функции s(t), то соответствующий ему комплексный сигнал представляется форме

z(t)=s(t)+is₁(t), (1.4)

где s₁{t) — функция, сопряженная по Гильберту сигналу s(t).

Определенная таким образом комплексная функция z(t) называется комплексным или аналитическим сигналом, соответствующим физическому сигналу s{t). Заметим, что и в выражении (1.3) мнимая часть комплексной функции является функцией, сопряженной по Гильберту действительной части.

При представлении s(t) и s₁(t) аналитический сигнал может быть записан следующим образом: (1.5)

Где (1.6)

представляет собой комплексную огибающую узкополосного сиг­ала s(t).

Применение понятия об аналитическом сигнале дает ряд преимуществ при анализе сложных сигналов.

Рассмотрим основные свойства аналитического сигнала.

а) Спектр аналитического сигнала содержит только положительные частоты.

Из выражения z(t)=s(t)+is₁(t) вытекает, что спектральная плотность Z(ω) аналитического сигнала z(t) определяется суммой Z(ω) = S(ω) + iS₁(ω). (1.7)

Но при ω>0 S₁(ω)= -iS(ω), а при ω<0 S₁(ω)= iS₁(ω).

Следовательно, (1.8)

Так, например, если узкополосному сигналу s(t) соответствует спектральная плотность S(ω), модуль которой изображен на рис.1.1 пунктиром, то аналитическому сигналу z(t)=s(t)+is₁(t) соответ­ствует спектральная плотность Z(ω), изображенная на том же рисун­ке сплошной линией (модуль).

Интеграл Фурье для аналитического сигнала z(t) принимает сле­дующий вид:

(1.9)

где S(ω) - спектральная плотность исходного (физического) сигнала s(t).

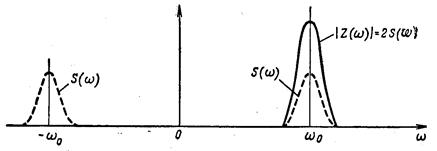
Рис.1.1. Спектральная плотность аналитического сигнала

Из соотношений (1.9) вытекает, что комплексная функция A(t) не является аналитическим сигналом. Действительно, спектр фун­кции A(t), получающийся из спектра Z(ω) сдвигом последнего на величину ω₀ (влево), в окрестности точки ω = 0 не может обра­щаться в нуль ни слева, ни справа от этой точки. Это объясняется тем, что действительная и мнимая части A(t) не являются функ­циями, сопряженными по Гильберту.

б) Произведение аналитического сигнала z(t) на сопряженный ему сигнал z*(t) равно квадрату огибающей исходного (физического) сигнала s(t).

Действительно, (1.10)

Таким образом, модуль аналитического сигнала z(t) равен просто огибающей сигнала s(t): (1.11)

в) Энергия Е_г аналитического сигнала z(t) равна удвоенной энергии Е_s исходного физического сигнала s(t).

Исходим из равенства Парсеваля с учетом формулы (1.8):

(1.12)

К этому результату можно прийти также и следующим путем:

(1.13)

Учитывая, что энергия сигнала s(t) = A (t) cos ψ(t) равна (1.14)

Получаем