Энергетический спектр случайного сигнала. Отличие от спектральной плотности детерминированного сигнала. Понятие белого шума. Дифференцирование и интегрирование случайного сигнала.

Подразумевая под случайным процессом множество (ансамбль) функций времени, необходимо иметь в виду, что функциям, имеющим различную фор­му, соответствуют различные спектральные характеристики. Усреднение комплексной спектральной плотности, определяемойой (1.47), по всем функциям приводит к нулевому спектру процесса (при М[х(t)]=0) из-за случайности и независимости фаз спектральных составляющих в различных реализациях. Можно, однако, ввести понятие спектральной плотности сред­него квадрата случайной функции, поскольку значение среднего квадрата не зависит от соотношения фаз суммируемых гармоник. Если под случай­ной функцией х(t) подразумевается электрическое напряжение или ток, то средний квадрат этой функции можно рассматривать как среднюю мощ­ность, выделяемую в сопротивлении 1 Ом. Эта мощность распределена по частотам в некоторой полосе, зависящей от механизма образования случай­ного процесса. Спектральная плотность средней мощности представляет со­бой среднюю мощность, приходящуюся на 1 Гц при заданной частоте ω. Размерность функции W(ω), являющейся отношением мощности к полосе частот, есть

Спектральную плотность случайного процесса можно найти, если из­вестен механизм образования случайного процесса. Применительно к шу­мам, связанным с атомистической структурой материи и электричества, эта задача будет позже. Здесь же мы ограничимся несколькими определениями общего характера.

Выделив из ансамбля какую-либо реализацию x_k(t) и ограничив ее дли­тельность конечным интервалом Т, можно применить к ней обычное преоб­разование Фурье и найти спектральную плотность X_kT(ω). Тогда энергию рассматриваемого отрезка реализации можно вычислить с помощью форму­лы: (1.152)

Разделив эту энергию на T, получим среднюю мощность k-й реализации на отрезке Т (1.153)

При увеличении Т энергия Э_кТ возрастает, однако отношение стремится к некоторому пределу. Совершив предельный переход , получим

где

(1.154)

представляет собой спектральную плотность средней мощности рассматри­ваемой k-й реализации.

В общем случае величина W_k(ω) должна быть усреднена по множеству реализаций. Ограничиваясь в данном случае рассмотрением стационарного и эргодического процесса, можно считать, что найденная усреднением по одной реализации функция W_k(ω) характеризует весь процесс в целом. Опуcкая индекс k, получаем окончательное выражение для средней мощности случайного процесса

где 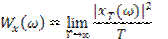(1.155)

Для процесса с нулевым средним (1.156)

Из определения спектральной плотности (1.155) очевидно, что W_х(ω) является четной и неотрицательной функцией ω.