Соотношение между спектральной плотностью и ковариационной функцией случайного процесса

С одной стороны, скорость изменения х(t) во времени определяет шири­ну спектра. С другой стороны, скорость изменения х (t) определяет ход ковариационной функции. Очевидно, что между W_х(ω) и К_х(τ) имеется тес­ная связь.

Теорема Винера — Хинчина утверждает, что К_х(τ) и W_x(ω) связаны между собой преобразованиями Фурье:

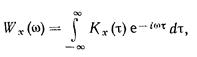(1.157)

(1.158)

Для случайных процессов с нулевым средним аналогичные выражения имеют вид

(1.159)

(1.160)

Из этих выражений вытекает свойство, аналогичное свойствам преобра­зований Фурье, для детерминированных сигналов: чем шире спектр случайного процесса, тем меньше интервал корреляции, и соответственно чем больше интервал корреляции, тем уже спектр процесса (см.рис.1.20).

Рис.1.20. Широкополосный и узкополосный спектры случайного процесса; границы центральной полосы : ±F₁

Большой интерес представляет белый шум, когда спектр равномерен на всех частотах .

Если в выражение 1.158 подставить W_x(ω) = W₀ = const, то получим

(1.161)

где δ(τ) — дельта-функция.

Для белого шума с бесконечным и равномерным спектром корреляцион­ная функция равна нулю для всех значений τ, кроме τ = 0, при котором R_x(0) обращается в бесконечность. Подобный шум, имеющий игольчатую структуру с бесконечно тонкими случайными выбросами, иногда называют дельта-коррелированным процессом. Дисперсия белого шума бесконечно велика.