И спектральная плотность.

Формирование сигнала конечной длительности (импульса) со строго равномерным спектром в заданной полосе частот невозможно. Однако можно получить хорошее приближение, используя псевдошумовые сложные сигналы, сигналы с внутриимпульсной частотной модуляцией, например, с линейной частотной модуляцией (ЛЧМ). Подобный сигнал изображен на рис 8,а, а закон изменения его частоты – на рис. 8,б.

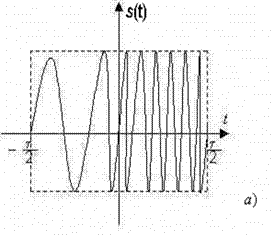
Мгновенная частота заполнения радиоимпульса соответствует выражению: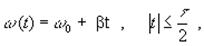

где t - длительность импульса, f _Д – амплитуда изменения (девиация) несущей частоты, b - скорость изменения частоты.

Мгновенное значение сигнала внутри импульса имеет вид:

Произведение 2f _Д t=B определяет базу ЛМЧ сигнала. С учетом этого обозначения имеет место:

Спектральная плотность такого сигнала равна:

Первое слагаемое полученного выражения определяет всплеск спектральной плотности вблизи частоты w =w ₀ , а второе – вблизи частоты w =-w ₀ . Поскольку АЧХ – функция четная, рассмотрим только первое слагаемое (положительные частоты).

Дополним до квадрата разности показатель степени:

,

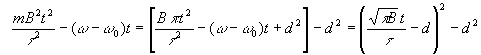где .

Аналогичное выражение можно получить и для второго слагаемого. Тогда спектральная плотность ЛЧМ импульса будет иметь вид: ,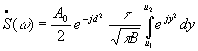

где - безразмерная переменная,

Интеграл в правой части определяется с помощью интегралов Френеля:

где

Откуда для области частот имеет место следующее:

где АЧХ ;

и ФЧХ:

Корреляционная функция на выходе фильтра, согласованного с ЛЧМ импульсом, будет иметь вид , что отображено на графике рис.

Огибающая автокорреляционной функции, и следовательно, выходной сигнал на выходе оптимального фильтра, образует очень острый пик (при ), а частота заполнения постоянна и равна центральной частоте . Штрих-пунктирной линией показана огибающая выходного радиоимпульса без частотной модуляции. Ясно, что ошибки обнаружения сигнала с ЛЧМ будут меньше.