Угловая модуляция.

Радиосигнал, несущий в себе информацию, можно представить в виде: 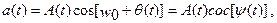(1.1)

в котором амплитуда А или фаза θ изменяются по закону передаваемого сообщения.

Если А или θ постоянные величины, то выражение (1.1.) описывает простое гармоническое колебание, не содержащее в себе никакой информации. Если А и θ подвергаются принудительному изменению для передачи сообщения, то колебание становится модулированным.

В зависимости от того, какой из двух параметров изменяется – амплитуда А или угол θ – различают 2 основных вида модуляции: амплитудную и угловую. Угловая модуляция, в свою очередь, подразделяется на 2 вида: частотную (ЧМ) и фазовую (ФМ). Эти два вида модуляции между собой тесно связаны, и различие между ними проявляется лишь в характере изменения во времени угла ψ при одной и той же модулирующей функции.

Модулированное колебание имеет спектр, структура которого зависит как от спектра передаваемого сообщения, так и от вида модуляции. То обстоятельство, что ширина спектра модулирующего сообщения мала по сравнению с несущей частотой , позволяет считать А(t) и θ(t) медленными функциями времени. Это означает, что относительные изменения А(t) и θ(t) за один период несущего колебания малы по сравнению с единицей.

При скорости изменения амплитуды приращение амплитуды за один период можно приближенно приравнять . Следовательно, относительное изменение за период равно (1.2)

Можно считать, что условие медленности функции А(t) выполняется, если 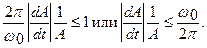(1.3)

Аналогичным образом можно установить условие медленности функции θ.

Так как мгновенная частота колебания равна скорости изменения фазы, то, дифференцируя аргумент выражения (1.1.), находим (1.4)

Производная определяет отклонение частоты от частоты . Это отклонение может быть быстрым или медленным. Для того, чтобы колебание можно было считать близким к гармоническому, нужно потребовать, чтобы изменение частоты за один цикл было мало по сравнению с частотой в рассматриваемый момент времени.

Таким образом, условие медленности функции θ(t) можно записать в виде следующего неравенства: (1.5)

Так как обычно очень мало отличается от , можно исходить из условия (1.6)

Для большинства используемых в радиотехнике сигналов неравенства (1.3) и (1.6) обычно выполняются. Это означает, что при любом виде модуляции параметры радиосигнала: амплитуда, фаза и частота - изменяются настолько медленно, что в пределах одного периода колебание можно считать гармоническим.